
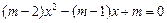 .(其中m为实数)
.(其中m为实数) 为y,求y与m的关系式;
为y,求y与m的关系式;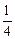 <m<2时,判断此方程的实数根的个数并说明理由
<m<2时,判断此方程的实数根的个数并说明理由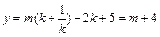
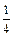 <m<2时,此方程有两个不相等的实数根
<m<2时,此方程有两个不相等的实数根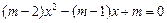 的实数根,
的实数根,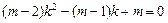 .※ …………………………………………1分
.※ …………………………………………1分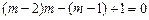 .
.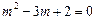 .
. 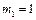 ,
,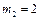 . ………………………………………………………2分
. ………………………………………………………2分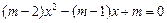 是关于x的一元二次方程,
是关于x的一元二次方程,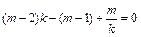 .…………………4分
.…………………4分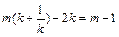 .
. 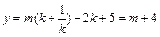 .……………………………………………5分
.……………………………………………5分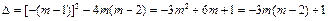 .………6分
.………6分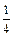 <m<2时,m>0,
<m<2时,m>0,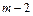 <0.
<0.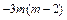 >0,
>0,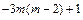 >1>0,Δ>0.
>1>0,Δ>0.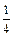 <m<2时,此方程有两个不相等的实数根. ……………7分
<m<2时,此方程有两个不相等的实数根. ……………7分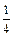 <m<2时,函数
<m<2时,函数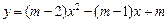 的图象,
的图象,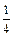 <m<2时,此方程有两个不相等的实数根. ……………7分
<m<2时,此方程有两个不相等的实数根. ……………7分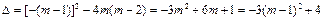 .…………6分
.…………6分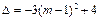 关于m的图象可知,(如图6)
关于m的图象可知,(如图6)
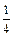 <m≤1时,
<m≤1时,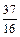 <
<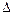 ≤4;
≤4;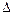 <4.
<4.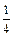 <m<2时,
<m<2时,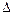 >0.
>0.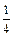 <m<2时,此方程有两个不相等的实数根.…7分
<m<2时,此方程有两个不相等的实数根.…7分

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:单选题
| A.x2-5x+5=0 | B.x2+5x+5="0" | C.x2+5x-5=0 | D.x2+5=0 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 2+b
2+b +c=0(a≠0)的两根分别为
+c=0(a≠0)的两根分别为 1、
1、 2,则有
2,则有 1+
1+ 2=
2= ;
; 1
1 2=
2=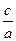 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com