
分析 (1)若传球1次,球有可能在乙手中,也有可能在丙手中,所以球在乙手中的概率为$\frac{1}{2}$.
(2)若传球3次,应用树状图法,求出球在甲手中的概率是多少即可.
解答 解:(1)∵传球1次,球有可能在乙手中,也有可能在丙手中,
∴球在乙手中的概率为$\frac{1}{2}$.
(2) ,
,
∵3次传球后,所有等可能的情况共有8种,其中球在甲手中的有2种情况,
∴若传球3次,求球在甲手中的概率是:$\frac{2}{8}$=$\frac{1}{4}$.
故答案为:$\frac{1}{2}$.
点评 此题主要考查了列表法与树状图法,要熟练掌握,解答此题的关键是要明确:树状图法一般是选择一个元素再和其它元素分别组合,依次列出,像树的枝丫形式,最末端的枝丫个数就是总的可能的结果n.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
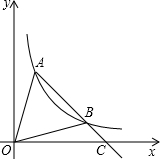 如图,A、B为反比例函数y=$\frac{k}{x}$(x>0)图象上的两点,A、B两点坐标分别为(m,5-m)、(n,5-n)(m<n),连接AB并延长交x轴于点C.
如图,A、B为反比例函数y=$\frac{k}{x}$(x>0)图象上的两点,A、B两点坐标分别为(m,5-m)、(n,5-n)(m<n),连接AB并延长交x轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据:$\sqrt{5}$≈2.24,$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据:$\sqrt{5}$≈2.24,$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com