
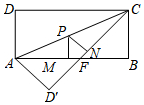
 如图,矩形ABCD中,AB=8,BC=4,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F.
如图,矩形ABCD中,AB=8,BC=4,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F.分析 (1)根据矩形的性质和翻折变换的性质得到AF=CF,设AF=x,根据勾股定理列出方程,解方程即可求出AF;
(2)根据三角形面积公式计算即可;
(3)连接PF,根据三角形的面积公式解答即可.
解答 解:(1)∵四边形ABCD是矩形,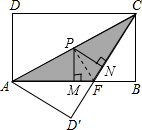
∴∠B=90°,AB∥CD,
∴∠DCA=∠BAC,
∵矩形沿AC折叠,点D落在点E处,
∴△ACD≌△ACE,
∴∠DCA=∠ECA,
∴∠BAC=∠ECA,
∴AF=CF,
设AF=CF=x,则BF=8-x,
在Rt△BCF中,根据勾股定理得:BC2+BF2=CF2,
即42+(8-x)2=x2,
解得:x=5,
∴AF=5;
(2)S△ACF=$\frac{1}{2}$AF•BC=$\frac{1}{2}$×5×4=10;
(3)连接PF,
$\frac{1}{2}$×AF×PM+$\frac{1}{2}$×CF×PN=S△ACF=10,
∴PM+PN=4.
点评 本题考查的是翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


科目:初中数学 来源: 题型:填空题
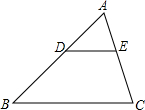 如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=4,BD=6,AE=3,那么AC=$\frac{15}{2}$.
如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=4,BD=6,AE=3,那么AC=$\frac{15}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
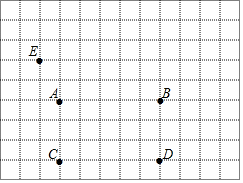 某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图,这是某校八(1)班教室简图,点A、B、C、D、E分别代表五个学习小组的位置.已知A点的坐标为(-1,3).
某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图,这是某校八(1)班教室简图,点A、B、C、D、E分别代表五个学习小组的位置.已知A点的坐标为(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
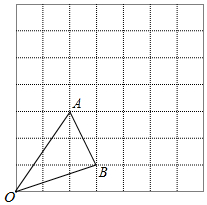 如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题:
如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
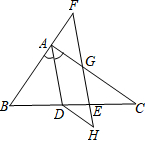 如图,AD平分∠BAC,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,且∠BDA=180°-∠CEG.
如图,AD平分∠BAC,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,且∠BDA=180°-∠CEG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com