
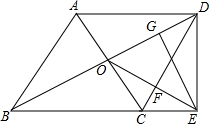
 如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,EG⊥BD,垂足为为G,连接DE.
如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,EG⊥BD,垂足为为G,连接DE.分析 (1)由平行四边形的性质得到BO=$\frac{1}{2}$BD,由等量代换推出OE=$\frac{1}{2}$BD,根据平行四边形的判定即可得到结论;
(2)根据等角的余角相等,得到∠CEO=∠CDE,推出△BDE∽△CDE,根据△CFE∽△DGE,得到$\frac{EG}{EF}$=$\frac{DE}{CE}$,等量代换得到$\frac{BD}{CD}$=$\frac{DE}{CE}$,即可得到结论.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴BO=OD,
∵OE=OB,
∴OE=OD,
∴∠OBE=∠OEB,∠OED=∠ODE,
∵∠OBE+∠OEB+∠OED+∠ODE=180°,
∴∠BEO+∠DEO=∠BED=90°,
∴DE⊥BE;
(2)∵OE⊥CD,
∴∠CEO+∠DCE=∠CDE+∠DCE=90°,
∴∠CEO=∠CDE,
∵OB=OE,
∴∠DBE=∠CDE,
∵∠BED=∠BED,
∴△BDE∽△DCE,
∴$\frac{BD}{CD}$=$\frac{DE}{CE}$,∠BDE=∠DCE,
∵∠DGE=∠CFE,
∴△CFE∽△DGE,
∴$\frac{EG}{EF}$=$\frac{DE}{CE}$,
∴$\frac{BD}{CD}$=$\frac{DE}{CE}$,
∴BD•EF=CD•EG.
点评 本题考查了相似三角形的判定和性质,直角三角形的判定和性质,平行四边形的性质,熟记定理是解题的关键.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:解答题
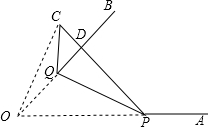 如图,∠AOB=45°,点P、Q分别是边OA、OB上的两点,且OP=2cm,将∠Q沿PQ折叠,点O落在平面内点C处,使得PQ=PD.
如图,∠AOB=45°,点P、Q分别是边OA、OB上的两点,且OP=2cm,将∠Q沿PQ折叠,点O落在平面内点C处,使得PQ=PD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
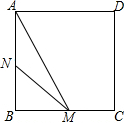 如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC-CD-DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )
如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC-CD-DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )| A. | 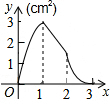 | B. | 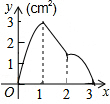 | C. | 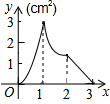 | D. | 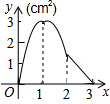 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 购买一张福利彩票中奖了 | |
| B. | 通常水加热到100℃时会沸腾 | |
| C. | 在地球上,抛出的篮球会下落 | |
| D. | 掷一枚骰子,向上一面的字数一定大于零 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com