
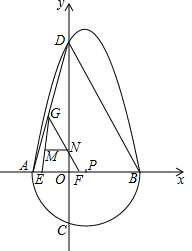
 ���ǰ�һ����Բ�������ߵ�һ���ֺϳɵķ��ͼ�γ�Ϊ����Բ������ͼ��A��B��C��D�ǡ���Բ����������Ľ��㣬��D������Ϊ��0��8������AB=6����P����ABΪֱ���İ�Բ��Բ�ģ�P������Ϊ��1��0��������DB��AD������E��F�ֱ��A��O�������������ͬ���ٶ���x���������˶�����F����B��ʱ����ͬʱֹͣ������F��FG��BD��AD�ڵ�G��
���ǰ�һ����Բ�������ߵ�һ���ֺϳɵķ��ͼ�γ�Ϊ����Բ������ͼ��A��B��C��D�ǡ���Բ����������Ľ��㣬��D������Ϊ��0��8������AB=6����P����ABΪֱ���İ�Բ��Բ�ģ�P������Ϊ��1��0��������DB��AD������E��F�ֱ��A��O�������������ͬ���ٶ���x���������˶�����F����B��ʱ����ͬʱֹͣ������F��FG��BD��AD�ڵ�G������ ��1����������������߽���ʽΪy=a��x+2����x-4�����ѵ�D��0��8�����뼴�����a��������⣮
��2���������������ۢ�D��ֱ�Ƕ��㣮��B��ֱ�Ƕ��㣮��H��ֱ�Ƕ��㣮�ֱ������H���꼴�ɣ�
��3������MN��ɨ����ͼ����ƽ���ı��Σ�����ƽ���ı��ε������ʽ���㼴�ɣ�
��� �⣺��1�������⣬D��0��8����A��-2��0����B��4��0����
�������߽���ʽΪy=a��x+2����x-4�����ѵ�D��0��8�������a=-1��
�������߽���ʽΪy=-x2+2x+8��
��2����ͼ1�У�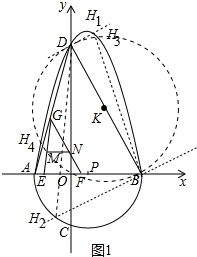
�ٵ�DΪֱ�Ƕ���ʱ��
��ֱ��BD����ʽΪy=-2x+8��
��DH1��BD��
��ֱ��DH1�Ľ���ʽΪy=$\frac{1}{2}$x+8��
��$\left\{\begin{array}{l}{y=\frac{1}{2}x+8}\\{y=-{x}^{2}+2x+8}\end{array}\right.$�����$\left\{\begin{array}{l}{x=0}\\{y=8}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{35}{4}}\end{array}\right.$��
���H1������$\frac{3}{2}$��$\frac{35}{4}$����
�ڵ�BΪֱ�Ƕ���ʱ��ֱ��BH2����ʽΪy=$\frac{1}{2}$x-2����H2��m��$\frac{1}{2}$m-2����
������PH2=3��
�ࣨm-1��2+��$\frac{1}{2}$m-2��2=9��
�����õ�5m2-16m-16=0��
���m=-$\frac{4}{5}$��4��
���H2������-$\frac{4}{5}$��-$\frac{12}{5}$����
�۵�HΪֱ�Ƕ���ʱ����H��m��-m2+2m+8����BD���е�K��2��4��
������HK=$\frac{1}{2}$BD=2$\sqrt{5}$��
�ࣨm-2��2+��-m2+2m+4��2=20��
��m��m-4����m2-3��=0��
��m=0��4��$��\sqrt{3}$��
��H3��$\sqrt{3}$��5+2$\sqrt{3}$����H4��������-$\sqrt{3}$��5-2$\sqrt{3}$����
�������������������ĵ�H������Ϊ��$\frac{3}{2}$��$\frac{35}{4}$����-$\frac{4}{5}$��-$\frac{12}{5}$����$\sqrt{3}$��5+2$\sqrt{3}$����-$\sqrt{3}$��5-2$\sqrt{3}$����
��3����ͼ3�У���M1N1����ʼλ�ã�M2N2S ��ֹλ�ã�
��M1N1��AB��M2N2��AB��
M1N1=$\frac{1}{2}$E1F1=1��M2N2=$\frac{1}{2}$E2F2=1��
��M1N1��M2N2��M1N1=M2N2��
���ı���M1N1N2M2��ƽ���ı��Σ���N1G��AB��J��N2H��AB��H��
��DN2=BN2��HN2��OD��
��OH=BH��
��HN2=$\frac{1}{2}$DO=4��
�ߡ�N1OJ=��N2BH����N1JO=��N2HB��
���N1JO�ס�N2HB��
��$\frac{{N}_{1}J}{{N}_{2}H}$=$\frac{O{N}_{1}}{B{N}_{2}}$��
��N1J=$\frac{4}{3}$��
��MN��ɨ����ͼ���������ƽ���ı���M1N1N2M2�����=1����4-$\frac{4}{3}$��=$\frac{8}{3}$��
���� ���⿼����κ����ۺ��⡢һ�κ�����ֱ�������ε��ж���ƽ���ı��ε��ж������ʡ����ɶ������������빫ʽ��֪ʶ������Ĺؼ������Ӧ����Щ֪ʶ������⣬ѧ��������ۣ�ѧ����������λ�ý�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| A�ͽ��ܵ綯�� | B�ͽ��ܵ綯�� | |
| �����۸���Ԫ/���� | 0.55 | 0.7 |
| ���ۼ۸���Ԫ/���� | 2016������ۼ۸� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x^6}{x^2}$=x3 | B�� | $\frac{x+y}{x+y}$=0 | C�� | $\frac{x+y}{{{x^2}+xy}}=\frac{1}{x}$ | D�� | $\frac{{2x{y^2}}}{{4{x^2}y}}=\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
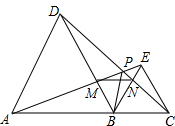 ��ͼ��A��B��C��һ��ֱ���ϣ���ABD����BCE��Ϊ�ȱ������Σ�����CD��AE���ڵ�P�����ֱ�BE��BD��N��M������MN�����н����У���AE=CD����AM=DP����MN��AC�� ����AB=2BC������DE����DE��BE����BPƽ�֡�APC����ȷ�Ľ����У��٢ۢܢݣ���д��������ȷ����ţ�
��ͼ��A��B��C��һ��ֱ���ϣ���ABD����BCE��Ϊ�ȱ������Σ�����CD��AE���ڵ�P�����ֱ�BE��BD��N��M������MN�����н����У���AE=CD����AM=DP����MN��AC�� ����AB=2BC������DE����DE��BE����BPƽ�֡�APC����ȷ�Ľ����У��٢ۢܢݣ���д��������ȷ����ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com