ŌĶĮĻĀĮŠ²ÄĮĻŌŁ»Ų“šĪŹĢā£ŗ
¶ŌÓŚŗÆŹży=x
2£¬µ±x=1Ź±£¬y=1£¬µ±x=-1Ź±£¬y=1£»µ±x=2Ź±£¬y=4£¬µ±x=-2Ź±£¬y=4£»”
¶ųµć£Ø1£¬1£©Óė£Ø-1£¬1£©£¬£Ø2£¬4£©Óė£Ø-2£¬4£©£¬”£¬¶¼¹ŲÓŚyÖį¶Ō³Ę£®ĻŌČ»£¬Čē¹ūµć£Øx
0£¬y
0£©ŌŚŗÆŹży=x
2µÄĶ¼ĻóÉĻ£¬ÄĒĆ“£¬Ėü¹ŲÓŚyÖį¶Ō³ĘµÄµć£Ø-x
0£¬y
0£©Ņ²ŌŚŗÆŹży=x
2µÄĶ¼ĻóÉĻ£¬ÕāŹ±£¬ĪŅĆĒĖµŗÆŹży=x
2¹ŲÓŚyÖį¶Ō³Ę£®
Ņ»°ćµŲ£¬Čē¹ū¶ŌÓŚŅ»øöŗÆŹż£¬µ±×Ō±äĮæxŌŚŌŹŠķ·¶Ī§ÄŚČ”ÖµŹ±£¬Čōx=x
0ŗĶx=-x
0Ź±£¬ŗÆŹżÖµ¶¼ĻąµČ£¬ĪŅĆĒĖµŗÆŹżµÄĶ¼Ļó¹ŲÓŚyÖį¶Ō³Ę£®
ĪŹĢā£ŗ
£Ø1£©¶ŌÓŚŗÆŹży=x
3£¬µ±×Ō±äĮæxČ”Ņ»¶ŌĻą·“ŹżŹ±£¬ŗÆŹżÖµŅ²µĆµ½Ņ»¶ŌĻą·“Źż£¬ŌņŗÆŹży=x
3µÄĶ¼Ļó¹ŲÓŚ
Ōµć
Ōµć
¶Ō³Ę£®£Ø”°xÖį”±”¢”°yÖį”±»ņ”°Ōµć”±£©£®
£Ø2£©ĻĀĮŠŗÆŹż£ŗ¢Ły=x
3+2x£»¢Śy=2x
4+4x
2£»¢Ū
y=x+£»¢Üy=-x
-2 ÖŠ£¬ĘäĶ¼Ļó¹ŲÓŚyÖį¶Ō³ĘµÄÓŠ
¢Ś¢Ü
¢Ś¢Ü
£¬¹ŲÓŚŌµć¶Ō³ĘµÄÓŠ
¢Ł¢Ū
¢Ł¢Ū
£ØÖ»ĢīŠņŗÅ£©£®
£Ø3£©ĒėÄ抓³öŅ»øöĪŅĆĒѧ¹żµÄŗÆŹż¹ŲĻµŹ½
£¬ĘäĶ¼Ļó¹ŲÓŚÖ±Ļßy=x¶Ō³Ę£®

 ŌĶĮĻĀĮŠ²ÄĮĻ£¬»Ų“šĪŹĢā£®
ŌĶĮĻĀĮŠ²ÄĮĻ£¬»Ų“šĪŹĢā£®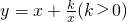 µÄŗÆŹż³ĘĪŖ”°øłŗÅŗÆŹż”±£¬ÕāĄąŗÆŹżµÄĶ¼Ļó¹ŲÓŚŌµćÖŠŠÄ¶Ō³Ę£®
µÄŗÆŹż³ĘĪŖ”°øłŗÅŗÆŹż”±£¬ÕāĄąŗÆŹżµÄĶ¼Ļó¹ŲÓŚŌµćÖŠŠÄ¶Ō³Ę£®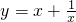 ŌŚµŚŅ»ĻóĻŽÄŚµÄ“óÖĀĶ¼ĻóČēĶ¼ĖłŹ¾£¬ŹŌŌŚĶųøńÄŚ»³öøĆŗÆŹżŌŚµŚČżĻóĻŽÄŚµÄ“óÖĀĶ¼Ļó£»
ŌŚµŚŅ»ĻóĻŽÄŚµÄ“óÖĀĶ¼ĻóČēĶ¼ĖłŹ¾£¬ŹŌŌŚĶųøńÄŚ»³öøĆŗÆŹżŌŚµŚČżĻóĻŽÄŚµÄ“óÖĀĶ¼Ļó£»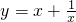 µÄ×īŠ”ÖµĪŖ2£®
µÄ×īŠ”ÖµĪŖ2£®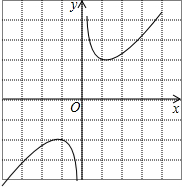
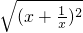 =
=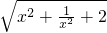 £¬
£¬ -2x•
-2x• =£Øx-
=£Øx- £©2”Ż0£¬
£©2”Ż0£¬ ”Ż2£¬
”Ż2£¬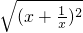 =
=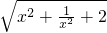 ”Ż
”Ż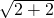 =2£¬
=2£¬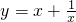 µÄ×īŠ”ÖµĪŖ2£®
µÄ×īŠ”ÖµĪŖ2£®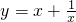 »ÆĪŖy=
»ÆĪŖy=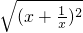 =
=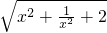 £¬ŌŁøł¾Ż²ÄĮĻ¶ž”¢ČżĖłøųĢõ¼ž½ā“š£®
£¬ŌŁøł¾Ż²ÄĮĻ¶ž”¢ČżĖłøųĢõ¼ž½ā“š£®

 ѧ¶ųÓÅĻĪ½Ó½Ģ²ÄÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø
ѧ¶ųÓÅĻĪ½Ó½Ģ²ÄÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø Š”ѧæĪĢĆ×÷ŅµĻµĮŠ“š°ø
Š”ѧæĪĢĆ×÷ŅµĻµĮŠ“š°ø ½š²©ŹæŅ»µćČ«ĶØĻµĮŠ“š°ø
½š²©ŹæŅ»µćČ«ĶØĻµĮŠ“š°ø
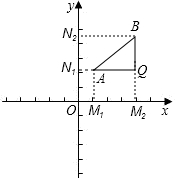 Ōµć£¬°ė¾¶ĪŖrµÄŌ²µÄ·½³Ģ£®
Ōµć£¬°ė¾¶ĪŖrµÄŌ²µÄ·½³Ģ£®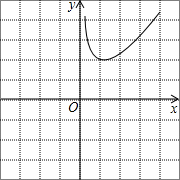 ŌĶĮĻĀĮŠ²ÄĮĻ£¬»Ų“šĪŹĢā£®
ŌĶĮĻĀĮŠ²ÄĮĻ£¬»Ų“šĪŹĢā£®