Question

13．在菱形ABCD中，∠ABC=α，其中点E、F分别在AD和BC上，将菱形ABCD沿EF折叠，点B落在边CD上的点N处，点A落在M点处．
（1）如图1，当α=144°，且FN∥BD时．求∠BND的度数；
（2）如图2，当α=90°时，MN与AD交于点H；
①若△DHN的周长等于8，求菱形ABCD的周长；
②若AB=4，CN=1，则△DHN的面积为$\frac{12}{5}$．

Answer 1

分析 （1）先利用菱形的性质，求得∠DBC=72°，∠C=36°，再根据轴对称的性质得出BF=NF，最后利用三角形外角性质，求得∠BND的度数；
（2）①先连接BH，过B作BG⊥MN于G，通过判定△BNC≌△BNG，△ABH≌△GBH，得出GN=CN，GH=AH，最后将△DNH的周长转化为AD+CD，求得菱形ABCD的周长；②设CF=x，在Rt△CFN中利用勾股定理求得CF的长，再判定△NCF∽△HDN，利用相似三角形对应边成比例，求得DH的长，最后计算△DNH的面积．

解答 解：（1）如图1，在菱形ABCD中，当∠ABC=α=144°时，∠DBC=72°，∠C=36°，
∵FN∥BD，
∴∠NFC=∠DBC=72°，
又∵BN被EF垂直平分，
∴BF=NF，
∴∠FBN=∠FNB=$\frac{1}{2}$∠NFC=36°，
∵∠BND是△BCN的外角，
∴∠BND=∠FBN+∠C=36°+36°=72°；

（2）①如图2，当∠ABC=α=90°时，菱形ABCD是正方形，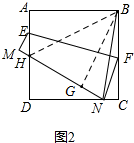
连接BH，过B作BG⊥MN于G，则∠BGN=90°，
由折叠得，∠FNG=90°=∠C，EF垂直平分BN，
∴∠FBN=∠FNB，
又∵∠FBN+∠BNC=90°，∠FNB+∠BNG=90°，
∴∠BNC=∠BNG，
在△BNC和△BNG中，
$\left\{\begin{array}{l}{∠BGN=∠C}\\{∠BNC=∠BNG}\\{BN=BN}\end{array}\right.$，
∴△BNC≌△BNG（AAS），
∴GN=CN，BG=BC=BA，
在Rt△ABH和Rt△GBH中，
$\left\{\begin{array}{l}{BH=BH}\\{BA=BG}\end{array}\right.$，
∴Rt△ABH≌Rt△GBH（HL），
∴GH=AH，
∴△DHN的周长=GH+DH+DN+GN=AH+DH+DN+CN=AD+CD，
又∵△DHN的周长等于8，
∴AD+CD=8
∴菱形ABCD的周长=2×8=16；

②当AB=4，CN=1时，BC=4，DN=3，
设CF=x，则BF=NF=4-x，
在Rt△CFN中，1²+x²=（4-x）²，
解得x=$\frac{15}{8}$，
即CF=$\frac{15}{8}$，
∵∠FNC+∠HND=90°，∠FNC+∠NFC=90°，
∴∠HND=∠NFC，
又∵∠D=∠C，
∴△NCF∽△HDN，
∴$\frac{NC}{HD}=\frac{CF}{DN}$，即$\frac{1}{HD}=\frac{\frac{15}{8}}{3}$，
解得HD=$\frac{8}{5}$，
∴△DHN的面积=$\frac{1}{2}$×DH×DN=$\frac{1}{2}$×$\frac{8}{5}$×3=$\frac{12}{5}$．
故答案为：$\frac{12}{5}$．

点评 本题主要考查了四边形的综合应用，解题时注意，如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用．在直角三角形中，运用勾股定理可以求得线段的长度．