
【题目】如图1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.
(1)求证:△AEF≌△BEC;
(2)判断四边形BCFD是何特殊四边形,并说出理由;
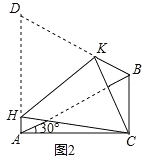
(3)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,若BC=1,求AH的长.

【答案】(1)(2)见解析;(3)![]()
【解析】试题分析:(1)在△ABC中,由已知可得∠ABC=60°,从而推得∠BAD=∠ABC=60°.由E为AB的中点,得到AE=BE.又因为∠AEF=∠BEC,所以△AEF≌△BEC;(2)在Rt△ABC中,E为AB的中点,则CE=![]() AB,BE=
AB,BE=![]() AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,则四边形BCFD是平行四边形.
AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,则四边形BCFD是平行四边形.
(2)由∠BAD=60°,∠CAB=30°,可得∠CAH=90°;在Rt△ABC中,∠CAB=30°,BC=1,根据30°角的直角三角形的性质可得AB=2BC=2,所以AD=AB=2.设AH=x,则HC=HD=AD﹣AH=2﹣x,在Rt△ABC中,由勾股定理求得AC2=3,在Rt△ACH中,根据勾股定理列出方程x2+3=(2﹣x)2,解方程即可求得AH的值.
试题解析:
(1)证明:①在△ABC中,∠ACB=90°,∠CAB=30°,∴∠ABC=60°.
在等边△ABD中,∠BAD=60°,∴∠BAD=∠ABC=60°.
∵E为AB的中点,∴AE=BE.又∵∠AEF=∠BEC,∴△AEF≌△BEC.
(2)在△ABC中,∠ACB=90°,E为AB的中点,
∴CE=![]() AB,BE=
AB,BE=![]() AB.∴CE=AE,∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°.
AB.∴CE=AE,∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°.
又∵△AEF≌△BEC,∴∠AFE=∠BCE=60°.
又∵∠D=60°,∴∠AFE=∠D=60°.∴FC∥BD.
又∵∠BAD=∠ABC=60°,∴AD∥BC,即FD∥BC.∴四边形BCFD是平行四边形
(3)∵∠BAD=60°,∠CAB=30°,∴∠CAH=90°.
在Rt△ABC中,∠CAB=30°,BC=1,∴AB=2BC=2.∴AD=AB=2.
设AH=x,则HC=HD=AD﹣AH=2﹣x,在Rt△ABC中,AC2=22﹣12=3,
在Rt△ACH中,AH2+AC2=HC2,即x2+3=(2﹣x)2,解得x=![]() ,即AH=
,即AH=![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以![]() cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA-AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),求在这一运动过程中y与x之间函数关系式.
cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA-AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),求在这一运动过程中y与x之间函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图: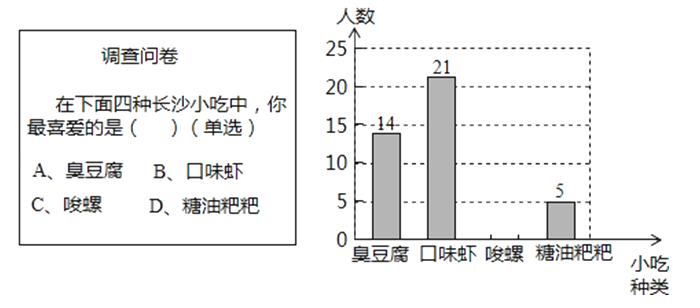
请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?
(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )

A. 1<MN<5 B. 1<MN≤5 C. ![]() <MN<
<MN<![]() D.
D. ![]() <MN≤
<MN≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A,B,C三名同学竞选学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图一
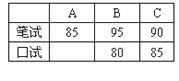
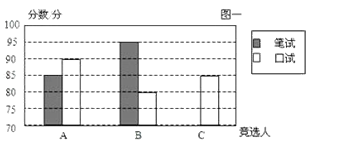
(1)请将表格和图一中的空缺部分补充完整;
(2)竞选的最后一个程序是由本校的300名学生代表进行投票,三位候选人的得票数分别为105票,120票,75票;若每票计1分,学校将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中有1个黑球和若干个白球,这些球除颜色外其他都相同.已知从中任意摸取一个球,摸得黑球的概率为![]() .
.
(1)求口袋中白球的个数;
(2)如果先随机从口袋中摸出一球,不放回,然后再摸出一球,求两次摸出的球都是白球的概率.用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=![]() ,b=
,b=![]() ,
,
求(2)中式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com