
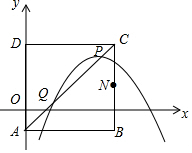
 在平面直角坐标系中,己知正方形ABCD的顶点A的坐标为(0,-1),点B的坐标为(4,-1),顶点C在第一象限内,抛物线y=-$\frac{1}{2}$x2+bx+c(b、c常数)的顶点P为正方形对角线AC上一动点.
在平面直角坐标系中,己知正方形ABCD的顶点A的坐标为(0,-1),点B的坐标为(4,-1),顶点C在第一象限内,抛物线y=-$\frac{1}{2}$x2+bx+c(b、c常数)的顶点P为正方形对角线AC上一动点.分析 (1)把A点和B点坐标代入y=-$\frac{1}{2}$x2+bx+c得到关于b、c的方程组,然后解方程组即可;
(2)先利用正方形性质得到C(4,3),再利用待定系数法求出直线AC的解析式为y=x-1,再求出顶点P的坐标为(b,c+$\frac{1}{2}$b2),然后把P(b,c+$\frac{1}{2}$b2)代入y=x-1得到b2-2b=-2c-2,设P(x1,x1-1),Q(x2,x2-1),则x1、x2为-$\frac{1}{2}$x2+bx+c=x-1的两根,利用根与系数的关系得到x1+x2=2(b-1),x1x2=-2-2c,然后利用两点间的距离公式计算PQ2=2(x1-x2)2=2[(x1+x2)2-4x1x2]=2[4(b-1)2-4(-2-2c)]=8(b2-2b+1+2+2c)=8,从而判定PQ长是定值;
(3)取AB的中点E,连接EN,DE,DE交AC于Q,如图,则EN=2$\sqrt{2}$,EN∥AC,则过N点作DE的平行线交AC于P,利用四边形QENP为平行四边形得到PN=QE,所以PN+QB=QE+DQ=DE,利用两点之间线段最短判断此时PN+QB的值最小,利用勾股定理可计算出它的最小值.
解答 (1)解:把A(0,-1),B(4,-1)代入y=-$\frac{1}{2}$x2+bx+c得$\left\{\begin{array}{l}{c=-1}\\{-8+4b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=\frac{9}{4}}\\{c=-1}\end{array}\right.$,
所以抛物线解析式为y=-$\frac{1}{2}$x2+$\frac{9}{4}$x-1;
(2)证明:∵四边形ABCD为正方形,
而AB=4,
∴C(4,3),
设直线AC的解析式为y=mx+n,
把A(0,-1),C(4,3)代入得$\left\{\begin{array}{l}{n=-1}\\{4m+n=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=1}\\{n=-1}\end{array}\right.$,
∴直线AC的解析式为y=x-1,
∵y=-$\frac{1}{2}$x2+bx+c=-$\frac{1}{2}$(x-b)2+c+$\frac{1}{2}$b2,
∴顶点P的坐标为(b,c+$\frac{1}{2}$b2),
把P(b,c+$\frac{1}{2}$b2)代入y=x-1得P的坐标c+$\frac{1}{2}$b2=b-1,即b2-2b=-2c-2,
设P(x1,x1-1),Q(x2,x2-1),
则x1、x2为-$\frac{1}{2}$x2+bx+c=x-1的两根,
整理为x2-2(b-1)x-2-2c=0,
∴x1+x2=2(b-1),x1x2=-2-2c,
∴PQ2=(x1-x2)2+(x1-x2)2=2(x1-x2)2=2[(x1+x2)2-4x1x2]=2[4(b-1)2-4(-2-2c)]=8(b2-2b+1+2+2c)=8(-2-2c+1+2+2c)=8,
∴PQ=2$\sqrt{2}$,
即PQ长是定值;
(3)取AB的中点E,连接EN,DE,DE交AC于Q,如图,
∵BE=2,BN=2,
∴EN=2$\sqrt{2}$,
∵EN∥AC,
∴过N点作DE的平行线交AC于P,
∴四边形QENP为平行四边形,
∴PN=QE,
∵点B与点D关于AC对称,
∴QB=QD,
∴PN+QB=QE+DQ=DE,
此时PN+QB的值最小,最小值为$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和旋转的性质;会运用待定系数法求函数解析式;能应用两点之间线段最短解决路径最短问题;会运用勾股定理和两点间的距离公式计算线段的长.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 小鹏早晨到校发现作业忘带,就打电话叫爸爸立即把作业送到学校,小鹏也同时往家赶,两人相遇后,小鹏以原速度返回学校,爸爸则以原速度的$\frac{2}{3}$返回家.设爸爸行走的时间为x分钟,小鹏和爸爸两人之间的距离为y米,y与x的函数关系如图所示,则当小鹏回到学校时,爸爸还需要2.5分钟才能到家.
小鹏早晨到校发现作业忘带,就打电话叫爸爸立即把作业送到学校,小鹏也同时往家赶,两人相遇后,小鹏以原速度返回学校,爸爸则以原速度的$\frac{2}{3}$返回家.设爸爸行走的时间为x分钟,小鹏和爸爸两人之间的距离为y米,y与x的函数关系如图所示,则当小鹏回到学校时,爸爸还需要2.5分钟才能到家.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两种客车总的载客量不少于500人 | |
| B. | 两种客车总的载客量不超过500人 | |
| C. | 两种客车总的载客量不足500人 | |
| D. | 两种客车总的载客量恰好等于500人 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com