练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．计算：${（\frac{1}{2016}）^0}×{10^{-1}}$=$\frac{1}{10}$．

    分析 本题涉及零指数幂、负整数指数幂2个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．

    解答 解：${（\frac{1}{2016}）^0}×{10^{-1}}$
    =1×$\frac{1}{10}$
    =$\frac{1}{10}$．
    故答案为：$\frac{1}{10}$．

    点评 本题主要考查了实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握零指数幂、负整数指数幂等考点的运算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．分解因式：
    （1）x3-xy2．
    （2）m3-6m2+9m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

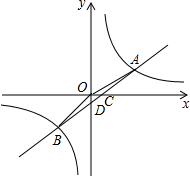    8．已知：如图所示，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数$y=\frac{k}{x}（k≠0）$的图象交于一、三象限内的A、B两点，与x交于点C，与y轴交于点D，OC=1，BC=5，$sin∠BCO=\frac{3}{5}$．
    （1）求该反比例函数和一次函数的解析式；
    （2）连接BO，AO，求△AOB的面积．
    （3）观察图象，直接写出不等式$ax+b＜\frac{k}{x}$的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．先化简，再求代数式$\frac{a+1}{a}$÷（a-$\frac{1+2a^2}{3a}$）的值，再选取一个合适的a值代入计算．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．把多项式ax2-4a分解因式的结果是a（x+2）（x-2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

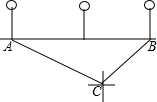    2．周末，小明一家去东昌湖划船，当船划到湖中C点处时，湖边的路灯A位于点C的北偏西64°方向上，路灯B位于点C的北偏东44°方向上，已知每两个路灯之间的距离是50米，求此时小明一家离岸边的距离是多少米？（精确到1米）（参考数据：
    sin64°≈0.9，cos64°≈0.4，tan64°≈2.1，sin44°≈0.7，cos44°≈0.7，tan44°≈1.0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，已知一次函数y1=kx+b（k≠0）的图象与反比例函数y2=-$\frac{8}{x}$的图象交于A、B两点，与坐标轴交于M、N两点．且点A的横坐标和点B的纵坐标都是-2．
    （1）求一次函数的解析式；
    （2）求△AOB的面积；
    （3）观察图象，直接写出y1＞y2时x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

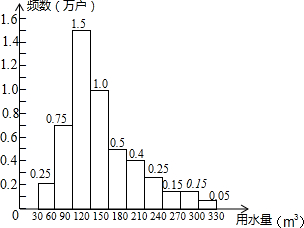    6．为了节约水资源，某市准备按照居民家庭年用水量实行阶梯水价．水价分档递增，计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%，15%和5%，为合理确定各档之间的界限，随机抽查了该市5万户居民家庭上一年的年用水量（单位：m3），绘制了统计图．如图所示，下面四个推断合理的是（　　）
    ①年用水量不超过180m3的该市居民家庭按第一档水价交费；
    ②年用水量超过240m3的该市居民家庭按第三档水价交费；
    ③该市居民家庭年用水量的中位数在150-180之间；
    ④该市居民家庭年用水量的平均数不超过180．
    A．①③B．①④C．②③D．②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．若点P（m，n）在直角坐标系的第二象限，则一次函数y=mx+n的大致图象是（　　）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案