
| 月用水量(吨) | 单价(元/吨) |
| 不大于10吨部分 | 1.5 |
| 大于10吨不大于m吨部分(10≤m≤50) | 2 |
| 大于m吨部分 | 3 |
分析 (1)用水20吨交费时包括两部分:10吨以内和超过10吨部分;
(2)利用水费的不同阶段的收费标准列出函数关系式即可;
(3)用40代替上题求得的函数的解析式,利用缴纳水费y元的取位范围为70≤y≤90得到有关m的不等式组,解得即可.
解答 解(1)∵20<m,
∴此时前面10吨每吨收1.5元,后面10吨每吨收2元,10×1.5+(20-10)×2=35(元),
答:其应缴纳的水费35元.
(2)①当x≤10时,y=1.5x,
②当10<x≤m时,y=10×1.5+(x-10)×2=2x-5,
③当x>m时,y=10×1.5+(m-10)×2+(x-m)×3=3x-m-5,
∴y=$\left\{\begin{array}{l}{1.5x(x≤10)}\\{2x-5(10<x≤m)}\\{3x-m-5(x>m)}\end{array}\right.$,
(3)∵10≤m≤50,
∴当用水量为40吨时就有可能是按照第二和第三两种方式收费,
①当40≤m≤50时,此时选择第二种方案,费用=2×40-5=75,符合题意,
②当10≤m<40时,此时选择第三种方案,费用=3x-m-5,
则:70≤3x-m-5≤90,
∴25≤m≤45,
∴此状况下25≤m≤40,
综合①、②可得m的取值范围为:25≤m≤50.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:填空题
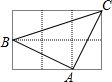 如图,小正方形边长为1,连接小正方形三个顶点,可得到△ABC,则:
如图,小正方形边长为1,连接小正方形三个顶点,可得到△ABC,则:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com