
在平面直角坐标系 中,已知二次函数
中,已知二次函数 的图象经过点
的图象经过点 和点
和点 ,直线
,直线 经过抛物线的顶点且与
经过抛物线的顶点且与 轴垂直,垂足为
轴垂直,垂足为 .
.
【小题1】求该二次函数的表达式;
【小题2】设抛物线上有一动点 从点
从点 处出发沿抛物线向上运动,其纵坐标
处出发沿抛物线向上运动,其纵坐标 随时间
随时间 ≥
≥ )的变化规律为
)的变化规律为 .现以线段
.现以线段 为直径作
为直径作 .
.
①当点 在起始位置点
在起始位置点 处时,试判断直线
处时,试判断直线 与
与 的位置关系,并说明理由;在点
的位置关系,并说明理由;在点 运动的过程中,直线
运动的过程中,直线 与
与 是否始终保持这种位置关系? 请说明你的理由;
是否始终保持这种位置关系? 请说明你的理由;
②若在点 开始运动的同时,直线
开始运动的同时,直线 也向上平行移动,且垂足
也向上平行移动,且垂足 的纵坐标
的纵坐标 随时间
随时间 的变化规律为
的变化规律为 ,则当
,则当 在什么范围内变化时,直线
在什么范围内变化时,直线 与
与 相交? 此时,若直线
相交? 此时,若直线 被
被 所截得的弦长为
所截得的弦长为 ,试求
,试求 的最大值.
的最大值.
【小题1】将点 和点
和点 的坐标代入,得
的坐标代入,得 ,解得
,解得 ,
,
∴二次函数的表达式为
【小题1】①当点 在点
在点 处时,直线
处时,直线 与
与 相切,理由如下:
相切,理由如下:
∵点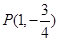 ,∴圆心的坐标为
,∴圆心的坐标为 ,∴
,∴ 的半径为
的半径为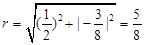 ,
,
又抛物线的顶点坐标为(0,-1),即直线l上所有点的纵坐标均为-1,从而圆心C到直线l的距离为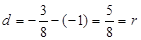 ,∴直线
,∴直线 与
与 相切.
相切.
在点 运动的过程中,直线
运动的过程中,直线 与
与 始终保持相切的位置关系,理由如下:
始终保持相切的位置关系,理由如下:
方法一: 设点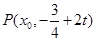 ,则圆心的坐标为
,则圆心的坐标为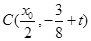 ,∴圆心C到直线l的距离为
,∴圆心C到直线l的距离为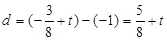 ,又∵
,又∵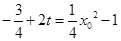 ,∴
,∴ ,则
,则 的半径为
的半径为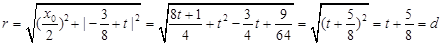 ,
,
∴直线 与
与 始终相切.
始终相切.
方法二: 设点 ≥1),则圆心的坐标为
≥1),则圆心的坐标为 ,
,
∴ 的半径为
的半径为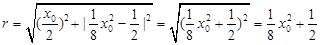 ,
,
而圆心C到直线l的距离为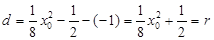 ,
,
∴直线 与
与 始终相切
始终相切
②由①知,圆C的半径为 .
.
又∵圆心C的纵坐标为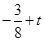 ,直线l上的点的纵坐标为
,直线l上的点的纵坐标为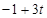 ,所以
,所以
(ⅰ)当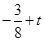 ≥
≥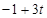 ,即
,即 ≤
≤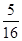 时,圆心C到直线l的距离为
时,圆心C到直线l的距离为 ,则由
,则由 ,得
,得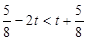 ,解得
,解得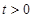 ,
,
∴此时 ≤
≤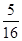 ;
;
(ⅱ)当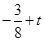 <
<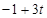 ,即
,即 >
>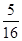 时,圆心C到直线l的距离为
时,圆心C到直线l的距离为 ,则由
,则由 ,得
,得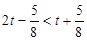 ,解得
,解得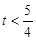 ,
,
∴此时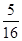 <
< ;
;
综上所述,当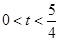 时,直线
时,直线 与
与 相交.
相交.
(说明: 若学生就写成 ≤
≤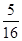 或
或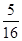 <
< ,得全分;若学生依据直观,只考虑圆心C在直线l下方的情况,解出
,得全分;若学生依据直观,只考虑圆心C在直线l下方的情况,解出 后,就得
后,就得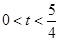 ,也给全分)
,也给全分)
∵当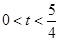 时,圆心C到直线l的距离为
时,圆心C到直线l的距离为 ,又半径为
,又半径为 ,
,
∴ ,
,
∴当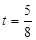 时,
时, 取得最大值为
取得最大值为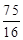 .
.
解析【小题1】所求函数的解析式中有两个待定系数,直接将A、B两点坐标代入即可得解.
【小题1】①由于OP是⊙C的直径,根据P点的纵坐标可表示出C点的纵坐标,进而能表示出C到直线l的距离;OP长易得,然后通过比较⊙C的半径和C到直线l的距离,即可判定直线l与⊙C的位置关系.
②该题要分两问来答,首先看第一问;该小题的思路和①完全一致,唯一不同的地方:要注意直线l与点C的位置关系(需要考虑到C到直线l的表达方式).
在第二问中,a2最大,那么a最大,即直线l被⊙C截得的弦最长(为直径),此时圆心C应在直线l上,根据该思路即可得解.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com