
分析 画树状图展示所有36种等可能的结果数,再利用二次函数的性质和一次函数的性质,找出满足条件关于x的函数y=(2a+5)x2+2x+b的图象不经过第四象限的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有36种等可能的结果数,其中满足条件关于x的函数y=(2a+5)x2+2x+b的图象不经过第四象限的结果数为15,
所以满足条件关于x的函数y=(2a+5)x2+2x+b的图象不经过第四象限的概率=$\frac{15}{36}$=$\frac{5}{12}$.
故答案为$\frac{5}{12}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.也考查了二次函数的性质.


科目:初中数学 来源: 题型:选择题
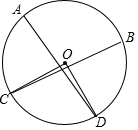 如图,已知在圆O中,劣弧AB的长度是周长的$\frac{1}{3}$,C与D在优弧AB上运动,连接AD与BC交于E点,当∠AEC=∠COD时,则∠COD=( )
如图,已知在圆O中,劣弧AB的长度是周长的$\frac{1}{3}$,C与D在优弧AB上运动,连接AD与BC交于E点,当∠AEC=∠COD时,则∠COD=( )| A. | 90° | B. | 45° | C. | 80° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com