
【题目】一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8, ![]() ≈1.732,结果取整数)
≈1.732,结果取整数)
【答案】解:辅助线如图所示:
BD⊥AD,BE⊥CE,CF⊥AF,
有题意知,∠FAB=60°,∠CBE=37°,
∴∠BAD=30°,
∵AB=20海里,
∴BD=10海里,
在Rt△ABD中,AD= ![]() =10
=10 ![]() ≈17.32海里,
≈17.32海里,
在Rt△BCE中,sin37°= ![]() ,
,
∴CE=BCsin37°≈0.6×10=6海里,
∵cos37°= ![]() ,
,
∴EB=BCcos37°≈0.8×10=8海里,
EF=AD=17.32海里,
∴FC=EF﹣CE=11.32海里,
AF=ED=EB+BD=18海里,
在Rt△AFC中,
AC= ![]() =
= ![]() ≈21.26海里,
≈21.26海里,
21.26×3≈64海里/小时.
答:救援的艇的航行速度大约是64海里/小时.
【解析】辅助线如图所示:BD⊥AD,BE⊥CE,CF⊥AF,在Rt△ABD中,根据勾股定理可求AD,在Rt△BCE中,根据三角函数可求CE,EB,在Rt△AFC中,根据勾股定理可求AC,
再根据路程÷时间=速度求解即可.
【考点精析】利用关于方向角问题对题目进行判断即可得到答案,需要熟知指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.


科目:初中数学 来源: 题型:
【题目】已知点D、E分别在△ABC的边AB、AC上,下列给出的条件中,不能判定DE∥BC的是( )
A.BD:AB=CE:AC
B.DE:BC=AB:AD
C.AB:AC=AD:AE
D.AD:DB=AE:EC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.
(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
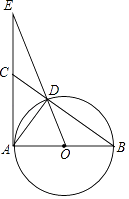
【题目】已知,如图,Rt△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于D,OD交AC的延长线于E,OA=1,AE=3.则下列结论正确的有 . ①∠B=∠CAD;②点C是AE的中点;③ ![]() =
= ![]() ;④tan B=
;④tan B= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4 ![]() 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
且∠AFG=60°,GE=2BG,则折痕EF的长为( ) 
A.1
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】志远要在报纸上刊登广告,一块10cm×5cm的长方形版面要付广告费180元,他要把该版面的边长都扩大为原来的3倍,在每平方厘米版面广告费相同的情况下,他该付广告费( )
A.540元
B.1080元
C.1620元
D.1800元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为2 ![]() ?若存在求出点Q的坐标;若不存在请说明理由.
?若存在求出点Q的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:x1 , x2是一元二次方程x2+2ax+b=0的两根,且x1+x2=3,x1x2=1,则a、b的值分别是( )
A.a=﹣3,b=1
B.a=3,b=1
C.![]() ,b=﹣1
,b=﹣1
D.![]() ,b=1
,b=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com