
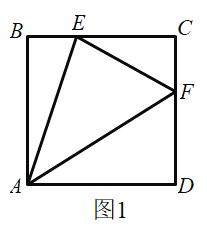
【题目】(1)如图1,在正方形![]() 中,点
中,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的动点,且
边上的动点,且![]() ,求证:
,求证:![]() .
.
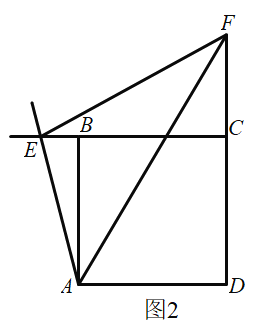
(2)如图2,在正方形![]() 中,如果点
中,如果点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 延长线上的动点,且
延长线上的动点,且![]() ,则
,则![]() 、
、![]() 、
、![]() 之间数量关系是什么?请写出证明过程.
之间数量关系是什么?请写出证明过程.
(3)如图1,若正方形![]() 的边长为6,
的边长为6,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ;证明见解析;(3)
;证明见解析;(3)![]() .
.
【解析】
(1)把![]() ABE绕点A顺时针旋转90°至
ABE绕点A顺时针旋转90°至![]() ADG,由“SAS”可证
ADG,由“SAS”可证![]() EAF≌
EAF≌![]() GAF,可得出EF=FG,则结论得证;
GAF,可得出EF=FG,则结论得证;
(2)将![]() ABE绕点A顺时针旋转90°至△ADM,根据SAS可证明
ABE绕点A顺时针旋转90°至△ADM,根据SAS可证明![]() EAF≌
EAF≌![]() MAF,可得EF=FM,则结论得证;
MAF,可得EF=FM,则结论得证;
(3)由全等三角形的性质可得AE=AG=3![]() ,EF=FG,BE=DG,由勾股定理可求DG的长,FD的长,AF的长.
,EF=FG,BE=DG,由勾股定理可求DG的长,FD的长,AF的长.
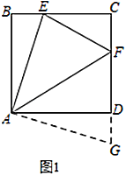
(1)证明:把![]() 绕点
绕点![]() 顺时针旋转90°至
顺时针旋转90°至![]() ,
,
如图1,∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
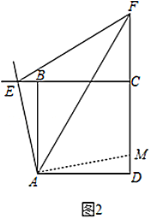
(2)结论:![]() ;
;
证明:如图2,将![]() 绕点
绕点![]() 顺时针旋转90°至
顺时针旋转90°至![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)解:由(1)可知![]() ,
,
∵正方形![]() 的边长为6,
的边长为6,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
解得:![]() .
.
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
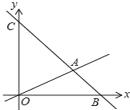
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据学习函数的经验,对函数y=x+![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
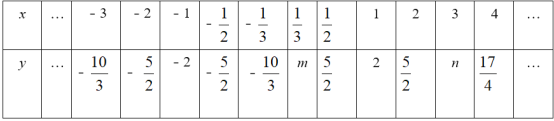
(2)下表列出了y与x的几组对应值,请写出m,n的值:m= ,n= ;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,请完成:
①当y=﹣![]() 时,x= .
时,x= .
②写出该函数的一条性质 .
③若方程x+![]() =t有两个不相等的实数根,则t的取值范围是 .
=t有两个不相等的实数根,则t的取值范围是 .
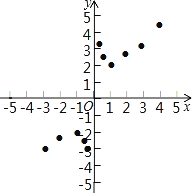
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,ABOC的顶点A(0,2),点B(﹣4,0),点O为坐标原点,点C在第一象限,若将△AOB沿x轴向右运动得到△EFG(点A、O、B分别与点E、F、G对应),运动速度为每秒2个单位长度,边EF交OC于点P,边EG交OA于点Q,设运动时间为t(0<t<2)秒.
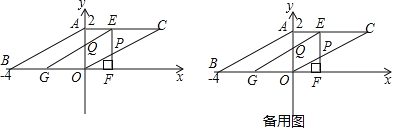
(1)在运动过程中,线段AE的长度为 (直接用含t的代数式表示);
(2)若t=1,求出四边形OPEQ的面积S;
(3)在运动过程中,是否存在四边形OPEQ为菱形?若存在,直接写出此时四边形OPEQ的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
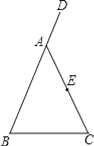
【题目】如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
(1)利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);
(2)试判断AF与BC有怎样的位置关系与数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一海轮位于灯塔P的西南方向,距离灯塔40了2海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
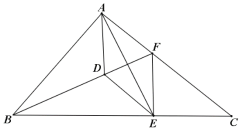
【题目】如图,点E,F分别在△ABC的边BC和AC上,点A,E关于BF对称.点D在BF上,且AD∥EF.
(1)求证:四边形ADEF为菱形;
(2)如果∠ABC=2∠DAE,AD=3,FC=5,求AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,AC是⊙O的直径,AD是⊙O的切线.点E在直径AC上,连接ED交⊙O于点B,连接AB,且AB=BD.
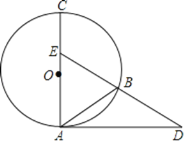
(1)求证:AB=BE;
(2)若⊙O的半径长为5,AB=6,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级数学模拟测试中,六名学生的数学成绩如下表所示,下列关于这组数据描述正确的是( )

A.众数是110B.方差是16
C.平均数是109.5D.中位数是109
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com