
【题目】下列说法正确的是( )
A.﹣1的相反数是1
B.﹣1的倒数是1
C.﹣1的平方根是1
D.﹣1的立方根是1
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).

(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是某手机生产厂第一季度三个月产量统计图,图②是这三个月的产量与第一季度总产量的比例分布统计图,统计员在制作图①、图②时漏填了部分数据.
(1)该厂二月份生产的手机产量占第一季度的比例为 %;
(2)求该厂三月份生产手机的产量;
(3)请求出图②中一月份圆心角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在﹣2,﹣3,4这三个数中任选2个数分别作为点P的横坐标和纵坐标.
(1)可得到的点得个数为 ;
(2)求过P点的正比例函数图象经过第二,四象限的概率(用树形图或列表法求解);
(3)过点P得正比例函数中,函数y随自变量x的增大而增大的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10m).

(1)如果所围成的花圃的面积为45m2,试求宽AB的长;
(2)按题目的设计要求,能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+kx+2k﹣4
(1)当k=2时,求出此抛物线的顶点坐标;
(2)求证:无论k为任何实数,抛物线都与x轴有交点,且经过x轴一定点;
(3)已知抛物线与x轴交于A(x1,0)、B(x2,0)两点(A在B的左边),|x1|<|x2|,与y轴交于C点,且S△ABC=15.问:过A,B,C三点的圆与该抛物线是否有第四个交点?试说明理由.如果有,求出其坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
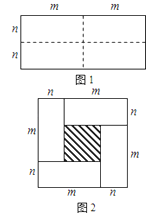
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请写出图2中阴影部分的面积;
(2)观察图2你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2, (m﹣n)2, mn;
(3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求(a﹣b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.

【答案】(1)画图见解析;(2)A(﹣2,0)B(0,4);(3)4;(4)x<﹣2.
【解析】试题分析:(1)求得一次函数y=2x+4与x轴、y轴的交点坐标,利用两点确定一条直线就可以画出函数图象;(2)由(1)即可得结论;(3)通过交点坐标根据三角形的面积公式即可求出面积;(4)观察函数图象与x轴的交点就可以得出结论.
试题解析:(1)当x=0时y=4,当y=0时,x=﹣2,则图象如图所示

(2)由上题可知A(﹣2,0)B(0,4),
(3)S△AOB=![]() ×2×4=4,
×2×4=4,
(4)x<﹣2.
考点:一次函数图象与系数的关系;一次函数的图象.
【题型】解答题
【结束】
21
【题目】在社会主义新农村建设中,衢州某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务有甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:

(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com