
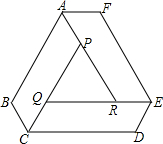
 如图,工人师傅要做一张由3块完全相同的平行四边形木板和1块三角板木板拼成的六边形桌面ABCDEF,量得AB=90cm,BC=30cm
如图,工人师傅要做一张由3块完全相同的平行四边形木板和1块三角板木板拼成的六边形桌面ABCDEF,量得AB=90cm,BC=30cm分析 (1)由平行四边形的性质就可以得出∠QPR=∠BAP.∠PQR=∠QCP,∠PRQ=∠REF.由全等形的性质就可以得出∠BAP=∠QCD=∠REF,CQ=BC,进而得出△PQR是等边三角形,由等边三角形的性质就可以求出结论;
(2)如图,过点P作PM⊥QR于M,过点Q作QN⊥CD于点N,由三角函数值就可以求出三角形的面积和一个平行四边形的面积,进而求出结论.
解答 解:(1)∵四边形ABCP是平行四边形,
∴AB∥CP,CP=AB=90,BC=AP=30°,
∴∠QPR=∠BAP.
同理:∠PQR=∠QCP,∠PRQ=∠REF.
∵平行四边形ABCP≌平行四边形CDEQ≌平行四边形EFRQ,
∴∠BAP=∠QCD=∠REF,CQ=BC=30,
∴∠QPR=∠PQR=∠PRQ,
∴△PQR是等边三角形,
∴∠QPR=∠PQR=∠PRQ=60°,PR=QR=PQ=CP-CQ=90-30=60,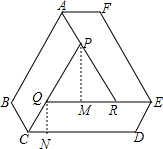
∴∠BAP=∠QPR=60°,
∴∠APC=180°-∠QPR=120°,
∴平行四边形木板各内角的度数为60°、120°、60°、120°;三角形木板各内角的度数都为60°,边长都为60cm;
(2)如图,过点P作PM⊥QR于M,过点Q作QN⊥CD于点N.
∵PQ=60,∠PQR=60°,
∴PM=PQ•sin60°=60×$\frac{\sqrt{3}}{2}$=30$\sqrt{3}$.
同理:QN=15$\sqrt{3}$.
∴S△PQR=$\frac{1}{2}$QR•PM=$\frac{1}{2}×60×30\sqrt{3}$=900$\sqrt{3}$,
S平行四边形CDEQ=CD•QN=90×15$\sqrt{3}$=1350$\sqrt{3}$,
∴六边形桌面ABCDEF的面积为:3×1350$\sqrt{3}$+90$\sqrt{3}$=4140$\sqrt{3}$cm2≈0.7m2.
点评 本题考查了平行四边形的性质的运用,等边三角形的判定及性质的运用,全等形的性质的运用,平行四边形的面积公式的运用,三角形的面积公式的运用,解答时运用全等形的性质求解是关键.


科目:初中数学 来源: 题型:选择题
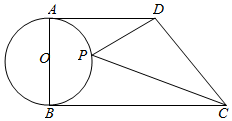 已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=5,AB=4,BC=8,则△PCD的面积的最小值是( )
已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=5,AB=4,BC=8,则△PCD的面积的最小值是( )| A. | 2 | B. | 4 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
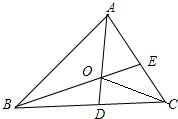 如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:
如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示的是某别墅的房顶人字架示意图,在△ABC中,AB=10cm,BC=10$\sqrt{3}$cm,BC边上的中线AD=5m.
如图所示的是某别墅的房顶人字架示意图,在△ABC中,AB=10cm,BC=10$\sqrt{3}$cm,BC边上的中线AD=5m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com