
”¾ĢāÄæ”æĖÄ“ØŹ”Ā«É½ĻŲ4ŌĀ20ČÕ·¢ÉśĮĖ7.0¼¶ĒæĮŅµŲÕš£¬Õžø®ĪŖĮĖ¾”æģ“ī½Ø°å·æ°²ÖĆŌÖĆń£¬øųij³§ĻĀ“ļĮĖÉś²śAÖÖ°å²Ä48000m2ŗĶBÖÖ°å²Ä24000m2µÄČĪĪń.
¢ÅČē¹ūøĆ³§°²ÅÅ280ČĖÉś²śÕāĮ½ÖÖ°å²Ä£¬ĆæČĖĆæĢģÄÜÉś²śAÖÖ°å²Ä60 m2»ņBÖÖ°å²Ä40 m2£¬ĒėĪŹ£ŗÓ¦·Ö±š°²ÅŶąÉŁČĖÉś²śAÖÖ°å²ÄŗĶBÖÖ°å²Ä£¬²ÅÄÜČ·±£Ķ¬Ź±Ķź³Éø÷×ŌµÄÉś²śČĪĪń£æ
¢ĘijŌÖĆń°²ÖƵć¼Ę»®ÓĆøĆ³§Éś²śµÄĮ½ÖÖ°å²Ä“ī½Ø¼×”¢ŅŅĮ½ÖÖ¹ęøńµÄ°å·æ¹²400¼ä£¬ŅŃÖŖ½ØÉčŅ»¼ä¼×ŠĶ°å·æŗĶŅ»¼äŅŅŠĶ°å·æĖłŠč°å²Ä¼°°²ÖĆČĖŹżČēĻĀ±ķĖłŹ¾£ŗ
°å·æ | AÖÖ°å²Ä(m2) | BÖÖ°å²Ä(m2) | °²ÖĆČĖŹż |
¼×ŠĶ | 110 | 61 | 12 |
ŅŅŠĶ | 160 | 53 | 10 |
¢Ł¹²ÓŠ¶ąÉŁÖֽط淽°øæɹ©Ń”Ōń£æ
¢ŚČōÕāøöŌÖĆń°²ÖƵćÓŠ4700ĆūŌÖĆńŠčŅŖ°²ÖĆ£¬Õā400¼ä°å·æÄÜ·ńĀś×ćŠčŅŖ£æČō²»ÄÜĀś×ćĒėĖµĆ÷ĄķÓÉ£»ČōÄÜĀś×ć£¬ĒėĖµĆ÷ӦєŌńŹ²Ć“·½°ø£®
”¾“š°ø”æ(1)°²ÅÅ160ČĖÉś²śAÖÖ°å²Ä£¬°²ÅÅ120ČĖÉś²śBÖÖ°å²Ä£»(2)¢Ł¹²ÓŠ31Öֽط淽°øæɹ©Ń”Ōń£»¢Ś½Ø¼×ŠĶ350¼ä£¬½ØŅŅŠĶ50¼äÄÜĀś×ćŠčŅŖ
”¾½āĪö”æ
£Ø1£©(1)Éč°²ÅÅxČĖÉś²śAÖÖ°å²Ä£¬Ōņ°²ÅÅ(280£x)ČĖÉś²śBÖÖ°å²Ä£¬øł¾ŻĢāŅāæÉĮŠ·ÖŹ½·½³Ģ£¬¼“æɽųŠŠĒó½ā£»£Ø2£©¢ŁÉč½Ø¼×ŠĶm¼ä£¬Ōņ½ØŅŅŠĶ(400£m)¼ä£¬øł¾ŻĢāŅāĮŠ³ö²»µČŹ½×飬¼“æÉĒó³ömµÄȔֵ£¬¼“æɵƵ½·½°øµÄøöŹż£»¢ŚÓÉĢāŅā£¬µĆ12m£«10(400£m)”Ż4700
½āµĆm”Ż350 £¬ŌŁøł¾Ż¢ŁĖłĒ󣬼“æÉÅŠ¶Ļ.
½ā£ŗ(1)Éč°²ÅÅxČĖÉś²śAÖÖ°å²Ä£¬Ōņ°²ÅÅ(280£x)ČĖÉś²śBÖÖ°å²Ä
øł¾ŻĢāŅā£¬µĆ![]()
½āµĆx£½160
¾¼ģŃéx£½160ŹĒŌ·½³ĢµÄøł£¬240£x£½120
”ą°²ÅÅ160ČĖÉś²śAÖÖ°å²Ä£¬°²ÅÅ120ČĖÉś²śBÖÖ°å²Ä
(2)Éč½Ø¼×ŠĶm¼ä£¬Ōņ½ØŅŅŠĶ(400£m)¼ä
¢Łøł¾ŻĢāŅā£¬µĆ![]()
½āµĆ320”Üm”Ü350
”ßmŹĒÕūŹż
”ą·ūŗĻĢõ¼žµÄmÖµÓŠ31øö
”ą¹²ÓŠ31Öֽط淽°øæɹ©Ń”Ōń
¢ŚÕā400¼ä°å·æÄÜĀś×ćŠčŅŖ
ÓÉĢāŅā£¬µĆ12m£«10(400£m)”Ż4700
½āµĆm”Ż350
ӧ320ӆmӆ350
”ąm£½350
”ą½Ø¼×ŠĶ350¼ä£¬½ØŅŅŠĶ50¼äÄÜĀś×ćŠčŅŖ


 µŚČżŃ§ĘŚÓ®ŌŚŹī¼ŁĻµĮŠ“š°ø
µŚČżŃ§ĘŚÓ®ŌŚŹī¼ŁĻµĮŠ“š°ø ѧĮ·æģ³µµĄæģĄÖ¼ŁĘŚŹī¼Ł×÷ŅµŠĀ½®ČĖĆń³ö°ęÉēĻµĮŠ“š°ø
ѧĮ·æģ³µµĄæģĄÖ¼ŁĘŚŹī¼Ł×÷ŅµŠĀ½®ČĖĆń³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
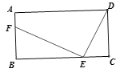
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬AB=m,BC=8£¬EĪŖĻ߶ĪBCÉĻµÄ¶Æµć£Ø²»ÓėB£¬CÖŲŗĻ£©£¬Į¬½ÓDE£¬×÷EF”ĶDE£¬EFÓėÉäĻßBA½»ÓŚµć£Ę£¬Éč£Ć£Å£½x,BF=y,Čō![]() £¬µ±DEFĪŖµČŃüČż½ĒŠĪŹ±,mµÄÖµĪŖ_________.
£¬µ±DEFĪŖµČŃüČż½ĒŠĪŹ±,mµÄÖµĪŖ_________.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĮāŠĪABCDÖŠ£¬¶Ō½ĒĻßACÓėBDĻą½»ÓŚµćO£¬AB=13£¬BD=24£¬ŌŚĮāŠĪABCDµÄĶā²æŅŌABĪŖ±ß×÷µČ±ßČż½ĒŠĪ ABE£®µćFŹĒ¶Ō½ĒĻßBDÉĻŅ»¶Æµć£ØµćF²»ÓėµćBÖŲŗĻ£©£¬½«Ļ߶ĪAFČʵćAĖ³Ź±Õė·½ĻņŠż×Ŗ60”ćµĆµ½Ļ߶ĪAM£¬Į¬½ÓFM£®
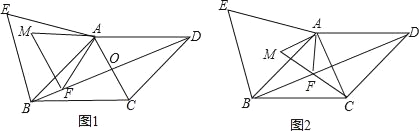
£Ø1£©ĒóAOµÄ³¤£»
£Ø2£©ČēĶ¼2£¬µ±µćFŌŚĻ߶ĪBOÉĻ£¬ĒŅµćM£¬F£¬CČżµćŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻŹ±£¬ĒóÖ¤£ŗAC=![]() AM£»
AM£»
£Ø3£©Į¬½ÓEM£¬Čō”÷AEMµÄĆ껿ĪŖ40£¬ĒėÖ±½ÓŠ“³ö”÷AFMµÄÖܳ¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
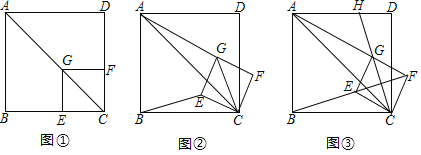
”¾ĢāÄæ”æČēĶ¼![]() £¬ŅŃÖŖµćGŌŚÕż·½ŠĪABCDµÄ¶Ō½ĒĻßACÉĻ£¬
£¬ŅŃÖŖµćGŌŚÕż·½ŠĪABCDµÄ¶Ō½ĒĻßACÉĻ£¬![]() £¬“¹×ćĪŖµćE£¬
£¬“¹×ćĪŖµćE£¬![]() £¬“¹×ćĪŖµćF£®
£¬“¹×ćĪŖµćF£®
![]() ·¢ĻÖĪŹĢā£ŗŌŚĶ¼
·¢ĻÖĪŹĢā£ŗŌŚĶ¼![]() ÖŠ£¬
ÖŠ£¬![]() µÄÖµĪŖ______£®
µÄÖµĪŖ______£®
![]() Ģ½¾æĪŹĢā£ŗ½«Õż·½ŠĪCEGFČʵćCĖ³Ź±Õė·½ĻņŠż×Ŗ
Ģ½¾æĪŹĢā£ŗ½«Õż·½ŠĪCEGFČʵćCĖ³Ź±Õė·½ĻņŠż×Ŗ![]() ½Ē
½Ē![]() £¬ČēĶ¼
£¬ČēĶ¼![]() ĖłŹ¾£¬Ģ½¾æĻ߶ĪAGÓėBEÖ®¼äµÄŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ½įĀŪ£®
ĖłŹ¾£¬Ģ½¾æĻ߶ĪAGÓėBEÖ®¼äµÄŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ½įĀŪ£®
![]() ½ā¾öĪŹĢā£ŗÕż·½ŠĪCEGFŌŚŠż×Ŗ¹ż³ĢÖŠ£¬µ±B£¬E£¬FČżµćŌŚŅ»ĢõÖ±ĻßÉĻŹ±£¬ČēĶ¼
½ā¾öĪŹĢā£ŗÕż·½ŠĪCEGFŌŚŠż×Ŗ¹ż³ĢÖŠ£¬µ±B£¬E£¬FČżµćŌŚŅ»ĢõÖ±ĻßÉĻŹ±£¬ČēĶ¼![]() ĖłŹ¾£¬ŃÓ³¤CG½»ADÓŚµćH£»Čō
ĖłŹ¾£¬ŃÓ³¤CG½»ADÓŚµćH£»Čō![]() £¬
£¬![]() £¬Ö±½ÓŠ“³öBCµÄ³¤¶Č£®
£¬Ö±½ÓŠ“³öBCµÄ³¤¶Č£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻC=90”ć£¬ŅŌACĪŖÖ±¾¶×÷”ŃO£¬½»ABÓŚD£¬¹żµćO×÷OE”ĪAB£¬½»BCÓŚE£®
£Ø1£©ĒóÖ¤£ŗEDĪŖ”ŃOµÄĒŠĻߣ»
£Ø2£©Čē¹ū”ŃOµÄ°ė¾¶ĪŖ![]() £¬ED=2£¬ŃÓ³¤EO½»”ŃOÓŚF£¬Į¬½ÓDF”¢AF£¬Ēó”÷ADFµÄĆ껿£®
£¬ED=2£¬ŃÓ³¤EO½»”ŃOÓŚF£¬Į¬½ÓDF”¢AF£¬Ēó”÷ADFµÄĆ껿£®

”¾“š°ø”æ£Ø1£©Ö¤Ć÷¼ū½āĪö£»£Ø2£©![]()
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©Ź×ĻČĮ¬½ÓOD£¬ÓÉOE”ĪAB£¬øł¾ŻĘ½ŠŠĻßÓėµČŃüČż½ĒŠĪµÄŠŌÖŹ£¬Ņ×Ö¤µĆ![]() ”Õ
”Õ![]() ¼“æɵĆ
¼“æɵĆ![]() £¬ŌņæÉÖ¤µĆ
£¬ŌņæÉÖ¤µĆ![]() ĪŖ
ĪŖ![]() µÄĒŠĻߣ»
µÄĒŠĻߣ»
£Ø2£©Į¬½ÓCD£¬øł¾ŻÖ±¾¶Ėł¶ŌµÄŌ²ÖܽĒŹĒÖ±½Ē£¬¼“æɵĆ![]() ĄūÓĆ¹“¹É¶ØĄķ¼“æÉĒóµĆ
ĄūÓĆ¹“¹É¶ØĄķ¼“æÉĒóµĆ![]() µÄ³¤£¬ÓÖÓÉOE”ĪAB£¬Ö¤µĆ
µÄ³¤£¬ÓÖÓÉOE”ĪAB£¬Ö¤µĆ![]() øł¾ŻĻąĖĘČż½ĒŠĪµÄ¶ŌÓ¦±ß³É±ČĄż£¬¼“æÉĒóµĆ
øł¾ŻĻąĖĘČż½ĒŠĪµÄ¶ŌÓ¦±ß³É±ČĄż£¬¼“æÉĒóµĆ![]() µÄ³¤£¬Č»ŗóĄūÓĆČż½ĒŗÆŹżµÄÖŖŹ¶£¬ĒóµĆ
µÄ³¤£¬Č»ŗóĄūÓĆČż½ĒŗÆŹżµÄÖŖŹ¶£¬ĒóµĆ![]() Óė
Óė![]() µÄ³¤£¬Č»ŗóĄūÓĆS”÷ADF=SĢŻŠĪABEF-SĢŻŠĪDBEFĒóµĆ“š°ø£®
µÄ³¤£¬Č»ŗóĄūÓĆS”÷ADF=SĢŻŠĪABEF-SĢŻŠĪDBEFĒóµĆ“š°ø£®
ŹŌĢā½āĪö£ŗ(1)Ö¤Ć÷£ŗĮ¬½ÓOD£¬

”ßOE”ĪAB£¬
”ą”ĻCOE=”ĻCAD£¬”ĻEOD=”ĻODA£¬
ӧOA=OD,
”ą”ĻOAD=”ĻODA£¬
”ą”ĻCOE=”ĻDOE£¬
ŌŚ”÷COEŗĶ”÷DOEÖŠ£¬
 ”ą”÷COE”Õ”÷DOE(SAS)£¬
”ą”÷COE”Õ”÷DOE(SAS)£¬
![]()
”ąED”ĶOD£¬
”ąEDŹĒ![]() µÄĒŠĻߣ»
µÄĒŠĻߣ»
(2)Į¬½ÓCD£¬½»OEÓŚM£¬
ŌŚRt”÷ODEÖŠ£¬
”ßOD=32£¬DE=2£¬
![]()
”ßOE”ĪAB£¬
”ą”÷COE”×”÷CAB£¬
![]() ”ąAB=5£¬
”ąAB=5£¬
”ßACŹĒÖ±¾¶£¬
![]()
![]()
![]()
![]()
”ßEF”ĪAB£¬
![]()
![]()
![]()
”ąS”÷ADF=SĢŻŠĪABEFSĢŻŠĪDBEF
![]()
”ą”÷ADFµÄĆ껿ĪŖ![]()

”¾ĢāŠĶ”æ½ā“šĢā
”¾½įŹų”æ
25
”¾ĢāÄæ”放ĢāÄæ”æŅŃÖŖ£¬Å×ĪļĻßy=ax2+ax+b£Øa”Ł0£©ÓėÖ±Ļßy=2x+mÓŠŅ»øö¹«¹²µćM£Ø1£¬0£©£¬ĒŅa£¼b£®
£Ø1£©ĒóbÓėaµÄ¹ŲĻµŹ½ŗĶÅ×ĪļĻߵĶ„µćD×ų±ź£ØÓĆaµÄ“śŹżŹ½±ķŹ¾£©£»
£Ø2£©Ö±ĻßÓėÅ×ĪļĻßµÄĮķĶāŅ»øö½»µć¼ĒĪŖN£¬Ēó”÷DMNµÄĆ껿ÓėaµÄ¹ŲĻµŹ½£»
£Ø3£©a=©1Ź±£¬Ö±Ļßy=©2xÓėÅ×ĪļĻßŌŚµŚ¶žĻóĻŽ½»ÓŚµćG£¬µćG”¢H¹ŲÓŚŌµć¶Ō³Ę£¬ĻÖ½«Ļ߶ĪGHŃŲyÖįĻņÉĻĘ½ŅĘtøöµ„Ī»£Øt£¾0£©£¬ČōĻ߶ĪGHÓėÅ×ĪļĻßÓŠĮ½øö²»Ķ¬µÄ¹«¹²µć£¬ŹŌĒótµÄȔֵ·¶Ī§£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ¾ŲŠĪABCDÖŠ£¬”ĻBµÄ½ĒĘ½·ÖĻßBEÓėAD½»ÓŚµćE£¬”ĻBEDµÄ½ĒĘ½·ÖĻßEFÓėDC½»ÓŚµćF£¬ČōAB=9£¬DF=2FC£¬ŌņBC=____£®£Ø½į¹ū±£ĮōøłŗÅ£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
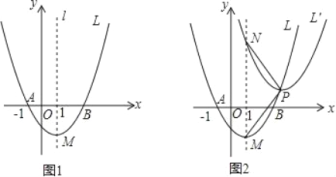
”¾ĢāÄæ”æČēĶ¼1£¬ŅŃÖŖÅ×ĪļĻßL£ŗy=ax2+bx©1.5(a£¾0)ÓėxÖį½»ÓŚµćA(-1,0)ŗĶµćB£¬¶„µćĪŖM£¬¶Ō³ĘÖįĪŖÖ±Ļßl£ŗx=1.
£Ø1£©Ö±½ÓŠ“³öµćBµÄ×ų±ź¼°Ņ»ŌŖ¶ž“Ī·½³Ģax2+bx©1.5=0µÄ½ā£®
£Ø2£©ĒóÅ×ĪļĻßLµÄ½āĪöŹ½¼°¶„µćMµÄ×ų±ź£®
£Ø3£©ČēĶ¼2£¬ÉčµćPŹĒÅ×ĪļĻßLÉĻµÄŅ»øö¶Æµć£¬½«Å×ĪļĻßLĘ½ŅĘ£®Ź¹ĖüµÄķµćŅĘÖĮµćP£¬µĆµ½ŠĀÅ×ĪļĻßL”䣬L”äÓėÖ±ĻßlĻą½»ÓŚµćN£®ÉčµćPµÄŗį×ų±źĪŖm
¢Łµ±m=5Ź±£¬PMÓėPNÓŠŌõŃłµÄŹżĮæ¹ŲĻµ£æĒėĖµĆ÷ĄķÓÉ£®
¢Śµ±mĪŖ“óÓŚ1µÄČĪŅāŹµŹżŹ±£¬¢ŁÖŠµÄ¹ŲĻµŹ½»¹³ÉĮ¢Āš£æĪŖŹ²Ć“£æ
¢ŪŹĒ·ń“ęŌŚÕāŃłµÄµćP£¬Ź¹”÷PMNĪŖµČ±ßČż½ĒŠĪ£æČō“ęŌŚ£®ĒėĒó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÕż·½ŠĪABCDÖŠ£¬µćEŹĒCDµÄÖŠµć£¬µćFŹĒBCÉĻµÄŅ»µć£¬ĒŅBF£½3CF£¬Į¬½ÓAE”¢AF”¢EF£¬ĻĀĮŠ½įĀŪ£ŗ¢Ł”÷ADE”×”÷ECF£¬¢Ś”ĻDAE£½”ĻEAF£¬¢ŪAE2£½ADAF£¬¢ÜS”÷AEF£½5S”÷ECF£¬ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ( )
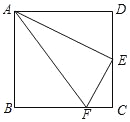
A. 1øöB. 2øöC. 3øöD. 4øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļß![]() ²»¾¹żµŚĖÄĻóĻŽ£¬ĒŅÓė
²»¾¹żµŚĖÄĻóĻŽ£¬ĒŅÓė![]() Öį£¬
Öį£¬![]() Öį·Ö±š½»ÓŚ
Öį·Ö±š½»ÓŚ![]() Į½µć£¬µć
Į½µć£¬µć![]() ĪŖ
ĪŖ![]() µÄÖŠµć£¬µć
µÄÖŠµć£¬µć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() ÉĻ£¬Ęä×ų±źĪŖ
ÉĻ£¬Ęä×ų±źĪŖ![]() £¬Į¬½į
£¬Į¬½į![]() £¬
£¬![]() £¬Čō
£¬Čō![]() £¬ÄĒĆ“
£¬ÄĒĆ“![]() µÄÖµĪŖ£Ø £©
µÄÖµĪŖ£Ø £©
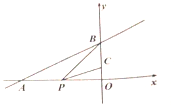
A. ![]() B. 4C. 5D. 6
B. 4C. 5D. 6
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com