
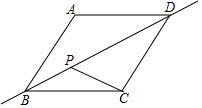
 如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+$\frac{PB}{2}$的值最小时,线段PD的长是( )
如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+$\frac{PB}{2}$的值最小时,线段PD的长是( )| A. | $\frac{4}{3}\sqrt{3}$ | B. | $\frac{2}{3}\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{4}{3}\sqrt{3}$ |
分析 先过P作PE⊥BC于E,连接AP,根据△ABP≌△CBP可得AP=CP,当点A,P,E在同一直线上时,AP+PE最短,此时,PC+$\frac{PB}{2}$的值最小,再根据含30°角的直角三角形的性质进行计算,即可得到线段PD的长.
解答  解:如图,过P作PE⊥BC于E,连接AP,
解:如图,过P作PE⊥BC于E,连接AP,
由菱形ABCD,可得AB=CB,∠ABP=∠CBP=∠ADP=30°,
∴△ABP≌△CBP,BP=2PE,
∴AP=CP,
∴PC+$\frac{PB}{2}$=AP+PE,
∵当点A,P,E在同一直线上时,AP+PE最短,
∴此时,PC+$\frac{PB}{2}$的值最小,AP⊥AD,
∵Rt△ABE中,AB=2,
∴BE=1,AE=$\sqrt{3}$,
∴Rt△BEP中,PE=$\frac{1}{3}\sqrt{3}$,
∴AP=$\frac{2}{3}\sqrt{3}$,
∵∠ADP=30°,
∴Rt△ADP中,PD=2AP=$\frac{4}{3}\sqrt{3}$,
故选:A.
点评 本题主要考查了菱形的性质以及最短路线问题,解决问题的关键是作辅助线构造直角三角形,解题时注意:凡是涉及最短距离的问题,一般要考虑线段的性质定理,多数情况要作点关于某直线的对称点.


科目:初中数学 来源: 题型:选择题
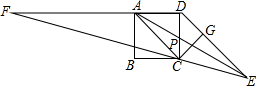 如图,四边形ABCD是正方形,DE∥AC,CE=AC,EC的延长线DA的延长线交于F,连AE交CD于P,作CG⊥DE于G,则下列结论:①AE平分∠CED;②S△ADP=S△EPC;③∠F=∠EAC;④CE=2CG.其中正确的说法有( )
如图,四边形ABCD是正方形,DE∥AC,CE=AC,EC的延长线DA的延长线交于F,连AE交CD于P,作CG⊥DE于G,则下列结论:①AE平分∠CED;②S△ADP=S△EPC;③∠F=∠EAC;④CE=2CG.其中正确的说法有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y3<y1<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com