
【题目】正方形ABCD中,对角线AC、BD交于O,Q为CD上任意一点,AQ交BD于M,过M作MN⊥AM交BC于N,连AN、QN.下列结论:①MA=MN;②∠AQD=∠AQN; ③S△AQN=![]() S五边形ABNQD;④QN是以A为圆心,以AB为半径的圆的切线.其中正确的结论有( )
S五边形ABNQD;④QN是以A为圆心,以AB为半径的圆的切线.其中正确的结论有( )

A. ①②③④ B. 只有①③④ C. 只有②③④ D. 只有①②
【答案】A
【解析】
延长CD到F,使DF=BN,连接AF,过A作AH⊥NQ于H,证A B N M四点共圆,推出∠ANM=∠NAM即可判断①;证△ABN≌△ADF,推出AF=AN,∠FAD=∠BAN,证△NAQ≌△FAQ,推出∠AQN=∠AQD即可判断②;证△ADQ≌△AHQ,即可推出③;根据AH=AD=AB,AH⊥NQ,即可判断④.
延长CD到F,使DF=BN,连接AF,过A作AH⊥NQ于H,

∵正方形ABCD,NM⊥AQ,
∴∠AMN=∠ABC=90°,
∴A B N M四点共圆,
∴∠NAM=∠DBC=45°,∠ANM=∠ABD=45°,
∴∠ANM=∠NAM=45°,
∴MA=MN,∴①正确;
∵正方形ABCD,
∴∠ABN=∠ADF=90°,AD=AB,
在△ABN和△ADF中,
∵ ,
,
∴△ABN≌△ADF,
∴∠FAD=∠BAN,AF=AN,
∵∠NAM=∠BAC=45°,
∴∠FAQ=∠FAD+∠DAQ=45°=∠NAQ,
在△NAQ和△FAQ中,
∵ ,
,
∴△NAQ≌△FAQ,
∴∠AQN=∠AQD,∴②正确;
在△ADQ和△AHQ中,
∵ ,
,
∴△ADQ≌△AHQ,
∴S△ADQ=S△AQH,
∴S△NAQ=S△FAQ=S△FAD+S△ADQ=![]() S五边形ABNQD,
S五边形ABNQD,
∴③正确;
∵AH=AD=AB,AH⊥NQ,
∴QN是以A为圆心,以AB为半径的圆的切线,
∴④正确.
故选:A.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】老师在讲完乘法公式![]() 的多种运用后,要求同学们运用所学知识解答:求代数式
的多种运用后,要求同学们运用所学知识解答:求代数式![]() 的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
解:![]()
∵![]() ,
,
当![]() 时,
时,![]() 的值最小,最小值是0,
的值最小,最小值是0,
∴![]()
当![]() 时,
时,![]() 的值最小,最小值是1,
的值最小,最小值是1,
∴![]() 的最小值是1.
的最小值是1.
请你根据上述方法,解答下列各题
(1)当x=______时,代数式![]() 的最小值是______;
的最小值是______;
(2)若![]() ,当x=______时,y有最______值(填“大”或“小”),这个值是______;
,当x=______时,y有最______值(填“大”或“小”),这个值是______;
(3)若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的点A、B、C、D、E表示连续的五个整数,对应数分别为a、b、c、d、e.
![]()
(1)若a+e=0,则代数式b+c+d= ;
(2)若a是最小的正整数,先化简,再求值:![]() ;
;
(3)若a+b+c+d=2,数轴上的点M表示的实数为m(m与a、b、c、d、e不同),且满足MA+MD=3,则m的范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 过A(2,3),B(4,3),C(6,﹣5)三点.
过A(2,3),B(4,3),C(6,﹣5)三点.
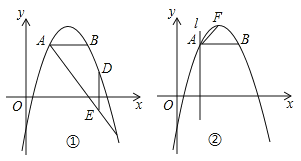
(1)求抛物线的表达式;
(2)如图①,抛物线上一点D在线段AC的上方,DE⊥AB交AC于点E,若满足![]() ,求点D的坐标;
,求点D的坐标;
(3)如图②,F为抛物线顶点,过A作直线l⊥AB,若点P在直线l上运动,点Q在x轴上运动,是否存在这样的点P、Q,使得以B、P、Q为顶点的三角形与△ABF相似,若存在,求P、Q的坐标,并求此时△BPQ的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程![]() 的两个根是
的两个根是![]() ,那么
,那么![]() ,反过来,如果
,反过来,如果![]() ,那么以
,那么以![]() 为两根的一元二次方程是
为两根的一元二次方程是![]() .请根据以上结论,解决下列问题:
.请根据以上结论,解决下列问题:
(1)已知关于x的方程![]() +mx+n=0(n≠0),求出—个一元二次方程,使它的两根分别是已知方程两根的倒数.
+mx+n=0(n≠0),求出—个一元二次方程,使它的两根分别是已知方程两根的倒数.
(2)已知a、b满足![]() -15a-5=0,
-15a-5=0,![]() -15b-5=0,求
-15b-5=0,求![]() 的值.
的值.
(3)已知a、b、c均为实数,且a+b+c=0,abc=16,求正数C的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于x的分式方程![]() =1的解为正数,求a的取值范围.
=1的解为正数,求a的取值范围.
经过独立思考与分析后,小杰和小哲开始交流解题思路如下:
小杰说:解这个关于x的分式方程,得x=a+4.由题意可得a+4>0,所以a>﹣4,问题解决.
小哲说:你考虑的不全面,还必须保证x≠4,即a+4≠4才行.
(1)请回答: 的说法是正确的,并简述正确的理由是 ;
(2)参考对上述问题的讨论,解决下面的问题:
若关于x的方程![]() 的解为非负数,求m的取值范围.
的解为非负数,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
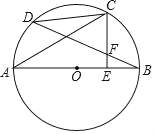
【题目】如图,AB是⊙O的直径,点C是弧BD的中点,CE⊥AB于点F.
(1)求证:BF=CF;
(2)若CD=3cm,AC=4cm,求⊙O的半径及CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
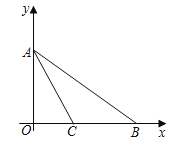
【题目】如图![]() ,在
,在![]() 中,
中,![]() 是原点,
是原点,![]() 是
是![]() 的角平分线.
的角平分线.
![]() 确定
确定![]() 所在直线的函数表达式;
所在直线的函数表达式;
![]() 在线段
在线段![]() 上是否有一点
上是否有一点![]() ,使点
,使点![]() 到
到![]() 轴和
轴和![]() 轴的距离相等,若存在,求出
轴的距离相等,若存在,求出![]() 点的坐标;若不存在,请说明理由;
点的坐标;若不存在,请说明理由;
![]() 在线段
在线段![]() 上是否有一点
上是否有一点![]() ,使点
,使点![]() 到点
到点![]() 和点
和点![]() 的距离相等,若存在,直接写出点
的距离相等,若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=kx+b交x轴于点A,交y轴于点B,直线y=2x﹣4交x轴于点D,与直线AB相交于点C(3,2).
(1)根据图象,写出关于x的不等式2x﹣4>kx+b的解集;
(2)若点A的坐标为(5,0),求直线AB的解析式;
(3)在(2)的条件下,求四边形BODC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com