
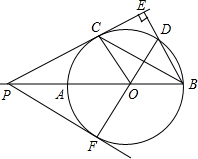
 如图,AB是⊙O的直径,延长BA至点P,过点P作⊙O的切线PC,切点为C,过点B向PC的延长线作垂线BE交该延长线于点E,BE交⊙O于点D,已知PA=1,PC=$\sqrt{3}$OC,
如图,AB是⊙O的直径,延长BA至点P,过点P作⊙O的切线PC,切点为C,过点B向PC的延长线作垂线BE交该延长线于点E,BE交⊙O于点D,已知PA=1,PC=$\sqrt{3}$OC,分析 (1)在直角△OPC中,利用勾股定理即可得到圆的半径长,然后利用相似三角形的性质求得BE的长;
(2)①证明△OBD是等边三角形,即可求得DE的长;
②首先证明△OPC≌△OPF,根据切线的判定定理即可证得.
解答  解:(1)设圆的半径是r,则OP=PA+r=1+r,OC=r,PC=$\sqrt{3}$r.
解:(1)设圆的半径是r,则OP=PA+r=1+r,OC=r,PC=$\sqrt{3}$r.
∵PC是圆的切线,
∴∠PCO=90°,
∴在直角△PCO中,PC2+OC2=OP2,即($\sqrt{3}$r)2+r2=(1+r)2,
解得:r=1或r=-$\frac{1}{3}$(舍去负值).
在直角△OPC中,cos∠POC=$\frac{OC}{OP}$=$\frac{1}{2}$,
∴∠POC=60°,
∵∠PCO=90°,BE⊥BC,
∴BE∥OC,
∴△OPC∽△BPE,∠B=∠POC=60°,
∴$\frac{OC}{BE}$=$\frac{OP}{BP}$=$\frac{2}{3}$,
∴BE=$\frac{2}{3}$OC=$\frac{3}{2}$;
(2)①在△OBD中,OB=OD,∠B=60°,
∴△OBD是等边三角形,BD=OB=1,∠BOD=60°.
∴DE=BE-BD=$\frac{3}{2}$-1=$\frac{1}{2}$;
②∵在△OPC和△OPF中,$\left\{\begin{array}{l}{OC=OF}\\{∠POF=∠BOD}\\{OP=OP}\end{array}\right.$,
∴△OPC≌△OPF(SAS),
∴∠OFP=∠OCP=90°,
∴PF是⊙O的切线.
点评 本题考查了相似三角形的判定与性质以及勾股定理、切线的判定、三角函数的综合应用,利用勾股定理求得圆的半径是关键.


科目:初中数学 来源: 题型:解答题
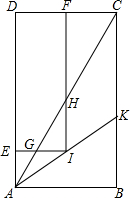 如图,已知矩形ABCD中,点I在∠CAB的平分线AK上运动,过I作IE⊥AD、IF⊥CD,垂足分别为E、F,IE、IF分别交AC于点G、H.
如图,已知矩形ABCD中,点I在∠CAB的平分线AK上运动,过I作IE⊥AD、IF⊥CD,垂足分别为E、F,IE、IF分别交AC于点G、H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上,从中随机抽取两张.
将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上,从中随机抽取两张.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com