

分析 (1)①根据tan∠ACE=$\frac{NE}{NC}=\frac{1}{2}$,只要证明MN=AN=CN即可解决问题.
②由△CNE∽△BCN,得$\frac{CE}{BN}=\frac{NE}{NC}=\frac{1}{2}$,即可解决问题.
(3)只要证明△MNC∽△ANM,即可解决问题$\frac{MN}{AN}$=$\frac{CM}{AM}$.
解答 解:(1)如图1中,
①∵AB=AC,∠ACB=90°,
∴∠A=45°,
∵MN⊥AC,
∴∠ANM=90°,
∴∠A=∠AMN=45°,
∴AN=MN,
∴$\frac{MN}{AN}=1$,
∴$\frac{NE}{AN}=\frac{1}{2}$,
∵MN∥BC,AM=BM,
∴AN=NC,
∴tan∠ACE=$\frac{NE}{NC}=\frac{1}{2}$.
②∵$\frac{BC}{CN}$=2,$\frac{CN}{NE}$=2,
∴$\frac{BC}{CN}$=$\frac{CN}{EN}$,
∵∠BCN=∠CNE=90°,
∴△CNE∽△BCN,
∴$\frac{CE}{BN}=\frac{NE}{NC}=\frac{1}{2}$.
(2)如图2中,连接CM.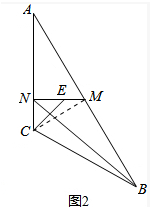
∵AC=BC,AM=BM,
∴CM⊥AB,
∵MN⊥AC,
∴∠ANM=∠MNC=90°,
∵∠AMN+∠NMC=90°,∠AMN+∠A=90°,
∴∠A=∠NMC,
∴△MNC∽△ANM,
∴$\frac{MN}{AN}$=$\frac{CM}{AM}$,
∴$\frac{\frac{1}{2}MN}{AN}$=$\frac{CM}{2AM}$,
即$\frac{EM}{AN}$=$\frac{CM}{AB}$,∵∠A=∠EMC,
∴△EMC∽△NAB,
∴$\frac{CE}{BN}$=$\frac{EM}{AM}$=$\frac{1}{2}m$.
点评 本题考查三角形综合题、相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形,学会利用两边成比例夹角相等的两个三角形相似,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 1.21% | B. | 8% | C. | 10% | D. | 12.1% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
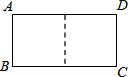 邻边不相等的矩形纸片,剪去一个最大的正方形,余下一个四边形,称为第一次操作,在余下的矩形纸片中再剪去一个最大的正方形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是正方形,则称原矩形为n阶方形,如图,矩形ABCD中,若AB=1,BC=2,则矩形ABCD为1阶方形.
邻边不相等的矩形纸片,剪去一个最大的正方形,余下一个四边形,称为第一次操作,在余下的矩形纸片中再剪去一个最大的正方形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是正方形,则称原矩形为n阶方形,如图,矩形ABCD中,若AB=1,BC=2,则矩形ABCD为1阶方形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com