
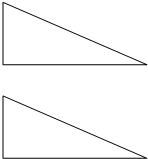
 将两个全等的直角三角形,拼成一个四边形.那么这些图形中有4个轴对称图形.
将两个全等的直角三角形,拼成一个四边形.那么这些图形中有4个轴对称图形.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
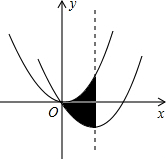 如图,在平面直角坐标系中,将抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为4.
如图,在平面直角坐标系中,将抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
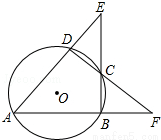 如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 实验与探究:三角点阵前n行的点数计算.
实验与探究:三角点阵前n行的点数计算.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
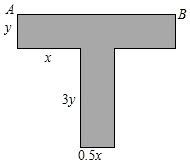 某种T型零件尺寸如图所示(左右宽度相同),求:
某种T型零件尺寸如图所示(左右宽度相同),求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com