
【题目】如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE. 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
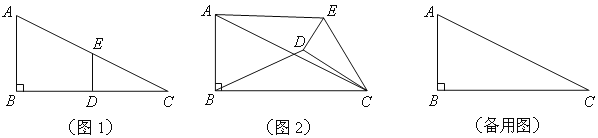
(1)问题发现
① 当![]() 时,
时,![]() ;
;
② 当![]() 时,
时,![]()
(2)拓展探究
试判断:当0°<α<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.
【答案】(1) ![]() .
.![]() .(2)
.(2) ![]() .(3)
.(3) ![]() 或
或![]() .
.
【解析】
试题分析:(1)①当α=0°时,在Rt△ABC中,由勾股定理,求出AC的值是多少;然后根据点D、E分别是边BC、AC的中点,分别求出AE、BD的大小,即可求出![]() 的值是多少.
的值是多少.
②α=180°时,可得AB∥DE,然后根据![]() ,求出
,求出![]() 的值是多少即可.
的值是多少即可.
(2)首先判断出∠ECA=∠DCB,再根据![]() ,判断出△ECA∽△DCB,即可求出
,判断出△ECA∽△DCB,即可求出![]() 的值是多少,进而判断出
的值是多少,进而判断出![]() 的大小没有变化即可.
的大小没有变化即可.
(3)根据题意,分两种情况:①点A,D,E所在的直线和BC平行时;②点A,D,E所在的直线和BC相交时;然后分类讨论,求出线段BD的长各是多少即可.
试题解析:(1)①当α=0°时,
∵Rt△ABC中,∠B=90°,
∴AC=![]() ,
,
∵点D、E分别是边BC、AC的中点,
∴AE=![]() ÷2=
÷2=![]() ,BD=8÷2=4,
,BD=8÷2=4,
∴![]() .
.
②如图1,
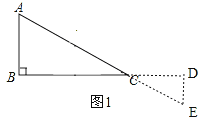 ,
,
当α=180°时,
可得AB∥DE,
∵![]() ,
,
∴![]() =
=![]() .
.
(2)如图2,
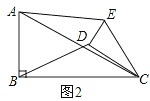 ,
,
当0°≤α<360°时,![]() 的大小没有变化,
的大小没有变化,
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵![]() =
=![]() ,
,
∴△ECA∽△DCB,
∴![]() .
.
(3)①如图3,
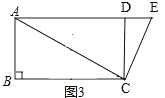 ,
,
∵AC=![]() ,CD=4,CD⊥AD,
,CD=4,CD⊥AD,
∴AD=![]() ,
,
∵AD=BC,AB=DC,∠B=90°,
∴四边形ABCD是矩形,
∴BD=AC=![]() .
.
②如图4,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,
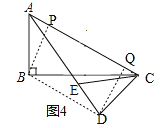 ,
,
∵AC=![]() ,CD=4,CD⊥AD,
,CD=4,CD⊥AD,
∴AD=![]() ,
,
∵点D、E分别是边BC、AC的中点,
∴DE=![]() AB=
AB=![]() ×(8÷2)=
×(8÷2)=![]() ×4=2,
×4=2,
∴AE=AD-DE=8-2=6,
由(2),可得
![]() ,
,
∴BD=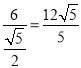 .
.
综上所述,BD的长为![]() 或
或![]() .
.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=![]() x2+3x+1的一部分,如图所示.
x2+3x+1的一部分,如图所示.
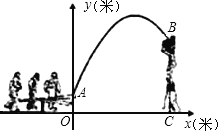
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面,如图,A、B、C、D、E、F所持的纸牌的前面分别写有六个算式:66;63+63;(63)3;(2×62)×(3×63);(22×32)3;(64)3÷62.游戏规定:所持算式的值相等的两个人是朋友.如果现在由同学A来找他的朋友,他可以找谁呢?说说你的看法.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,c2=2b 2,则两直角边a,b的关系是( )
A. a <b B. a >b C. a =b D. 以上三种情况都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线![]() 上运动,则k的值为( )
上运动,则k的值为( )
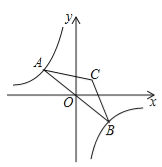
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com