
 如图,已知线段AB=4cm.
如图,已知线段AB=4cm.分析 (1)先根据AB=4cm,AB=2BC,求出BC的长,再延长线段AB到点C即可;
(2)在线段AC上标出点P,根据PB=PC-BC即可得出结论
(3)根据线段中点的性质和线段的和差,可得答案.
解答 解:(1)∵AB=4cm,AB=2BC
∴BC=$\frac{1}{2}$×4=2cm,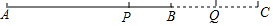
∴点C的位置如图所示;
(2)∵BC=2cm,
∴AC=AB+BC=4+2=6cm,
∵点P是线段AC的中点,
∴AP=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3cm,
∴PB=PC-BC=3-2=1cm;
(3)如图,
点P是线段AC的中点,点Q是BC的中点,得
PC=$\frac{1}{2}$AC=$\frac{1}{2}$(AB+BC),CQ=$\frac{1}{2}$BC,
由线段的和差,得
PQ=PC-CQ=$\frac{1}{2}$(AB+BC)-$\frac{1}{2}$BC=$\frac{1}{2}$AB,
又AB=4cm,
∴PQ=$\frac{1}{2}$×4=2cm.
点评 本题考查的是两点间的距离,熟知各线段之间的和、差关系是解答此题的关键.


科目:初中数学 来源: 题型:解答题
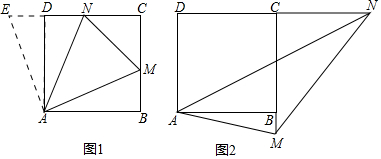
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
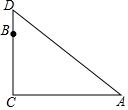 在一棵树的10米高处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高15米.
在一棵树的10米高处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高15米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
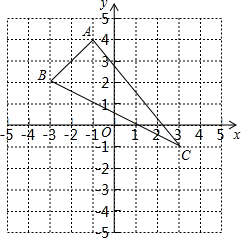 如图,已知△ABC的三个顶点分别为A(-1,4)、B(-3,2)、C(3,-1).
如图,已知△ABC的三个顶点分别为A(-1,4)、B(-3,2)、C(3,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com