

分析 (1)取同号的两数相乘,根据15>12即可得出结论;
(2)取异号的两数,将其绝对值相除,根据$\frac{3}{5}$<$\frac{4}{5}$<1<$\frac{5}{4}$<$\frac{4}{3}$<$\frac{5}{3}$即可得出结论;
(3)取+4将其放在指数位置,再根据(-3)4=34=81、(-5)4=625即可得出结论;
(4)取-3、-5、0、3,将其组成{0-[(-3)+(-5)]}×3=24,此题得解.
解答 解:(1)∵-3×(-5)=15,(+3)×(+4)=12,15>12,
∴抽取-3、-5两张卡片的乘积最大,最大值为15.
故答案为:-3、-5;15;
(2)∵$\frac{3}{5}$<$\frac{4}{5}$<1<$\frac{5}{4}$<$\frac{4}{3}$<$\frac{5}{3}$,
∴抽取-5、+3两张卡片相除的商最小,最小值为-$\frac{5}{3}$.
故答案为:-5、+3;-$\frac{5}{3}$.
(3)∵(-3)4=34=81,(-5)4=625,
∴抽取-5、4两张卡片,组成的最大值为(-5)4.
故答案为:-5、4;(-5)4.
(4)抽取-3、-5、0、3,则{0-[(-3)+(-5)]}×3=24.
故答案为:{0-[(-3)+(-5)]}×3=24.
点评 本题考查了有理数的混合运算以及有理数的乘方,熟练掌握有理数混合运算的运算方法及顺序是解题的关键


科目:初中数学 来源: 题型:解答题
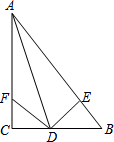 如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
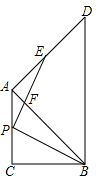 如图,已知△ABC和△ABD均为等腰直角三角形,∠ACB=∠BAD=90°,点P为边AC上任意一点(点P不与A、C两点重合),作PE⊥PB交AD于点E,交AB于点F.
如图,已知△ABC和△ABD均为等腰直角三角形,∠ACB=∠BAD=90°,点P为边AC上任意一点(点P不与A、C两点重合),作PE⊥PB交AD于点E,交AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2016x2016 | B. | 4029x2015 | C. | 4029x2016 | D. | 4031x2016 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com