
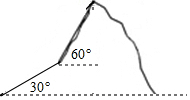
 如图,某人沿着30°的山坡前进1000m后侧得山顶的仰角为60°,又前进1500m便登上了山顶,求这座山的高度.(保留整数)
如图,某人沿着30°的山坡前进1000m后侧得山顶的仰角为60°,又前进1500m便登上了山顶,求这座山的高度.(保留整数) 分析 在Rt△ABC中根据sin∠BAC和AB的长求得BC=EF,在Rt△BDE中根据sin∠DBE和BD的长求得DE,即可得答案.
解答 解:如图,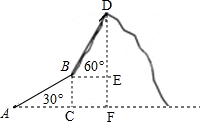
根据题意,知∠BAC=30°,AB=1000米,
∴EF=BC=ABsin∠BAC=1000×$\frac{1}{2}$=500(米),
∵∠DBE=60°,BD=1500米,
∴DE=BDsin∠DBE=1500×$\frac{\sqrt{3}}{2}$=750$\sqrt{3}$(米),
则山高为DE+EF=500+750$\sqrt{3}$≈1799,
答:山高为1799米.
点评 本题主要考查解直角三角形的应用,解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com