
分析 把被减数与减数约分后,再进行加减.
解答 ∵$\frac{2{x}^{2}+3x-2}{2{x}^{3}+{x}^{2}+3x-2}$
=$\frac{(2x-1)(x+2)}{(2{x}^{3}-{x}^{2})+(2{x}^{2}+3x-2)}$
=$\frac{(2x-1)(x+2)}{{x}^{2}(2x-1)+(2x-1)(x+2)}$
=$\frac{(2x-1)(x+2)}{(2x-1)({x}^{2}+x+2)}=\frac{x+2}{{x}^{2}+x+2}$
又∵$\frac{{x}^{2}-1}{{x}^{3}+x-2}=\frac{(x+1)(x-1)}{({x}^{3}-1)+(x-1)}$
=$\frac{(x+1)(x-1)}{(x-1)({x}^{2}+x+2)}=\frac{x+1}{{x}^{2}+x+2}$
∴原式=$\frac{x+2}{{x}^{2}+x+2}-\frac{x+1}{{x}^{2}+x+2}=\frac{1}{{x}^{2}+x+2}$
点评 本题考查了分式的加减、多项式的因式分解.被减数和减数的分式约分是解决本题的关键.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:填空题
 星晴天,小亮从家里骑自行车到同学家去玩,然后返回,如图是他离家的路程y(千米)与实际x(分钟)的函数图象,下列说法:
星晴天,小亮从家里骑自行车到同学家去玩,然后返回,如图是他离家的路程y(千米)与实际x(分钟)的函数图象,下列说法:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
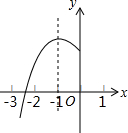 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论:| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读下列一段文字:已知在平面内两点P1(x1,y1)、P2(x2、y2),其两点间的距离P1P2=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
阅读下列一段文字:已知在平面内两点P1(x1,y1)、P2(x2、y2),其两点间的距离P1P2=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com