
 如图,抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A,B两点,点A的坐标为(-1,0),与y轴交于点C(0,-2).
如图,抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A,B两点,点A的坐标为(-1,0),与y轴交于点C(0,-2).分析 (1)将A(-1,0)代入y=$\frac{1}{2}$x2+bx-2,即可解出b的值,从而得到函数的解析式,配方后即可求出D点坐标;
(2)设点C关于x轴的对称点为C′,直线C′D的解析式为y=kx+n,由C′(0,2),D($\frac{3}{2}$,-$\frac{25}{8}$),利用待定系数法即可求得直线C′D的解析式,此直线与x轴的交点即为所求.
解答 解:(1)将A(-1,0)代入抛物线y=$\frac{1}{2}$x2+bx-2得,
$\frac{1}{2}$×(-1)2-b-2=0,
解得,b=-$\frac{3}{2}$,
则函数解析式为y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2.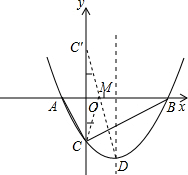
配方得,y=$\frac{1}{2}$(x-$\frac{3}{2}$)2-$\frac{25}{8}$,
可见,顶点坐标为($\frac{3}{2}$,-$\frac{25}{8}$).
(2)设点C关于x轴的对称点为C′,直线C′D的解析式为y=kx+n,
则$\left\{\begin{array}{l}{n=2}\\{\frac{3}{2}k+n=-\frac{25}{8}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{n=2}\\{k=-\frac{41}{12}}\end{array}\right.$.
∴y=-$\frac{41}{12}$x+2.
∴当y=0时,-$\frac{41}{12}$x+2=0,
解得:x=$\frac{24}{41}$.
∴m=$\frac{24}{41}$.
点评 本题考查了待定系数法求二次函数解析式、二次函数的性质、二次函数图象与几何变换的综合应用.掌握待定系数法求函数的解析式是解此题的关键,掌握辅助线的作法以及数形结合思想与方程思想的应用.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-a3)2=a6 | B. | a2•a3=a6 | C. | ($\frac{1}{2}$)-1-22=-2 | D. | (cos60°-$\frac{1}{2}$)0=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
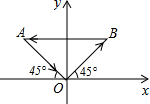 一艘快艇的航线如图所示,从O港出发,1小时后回到O港,若行驶中快艇的速度保持不变,AB∥x轴,则快艇驶完AB这段路程所用的时间为( )(取$\sqrt{2}$的值为1.4)
一艘快艇的航线如图所示,从O港出发,1小时后回到O港,若行驶中快艇的速度保持不变,AB∥x轴,则快艇驶完AB这段路程所用的时间为( )(取$\sqrt{2}$的值为1.4)| A. | 26分 | B. | 25分 | C. | 24分 | D. | 23分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查一沓钞票中有没有假钞 | B. | 调查我市中学生课外阅读的时间 | ||
| C. | 调查本市居民的年人均消费 | D. | 调查某种灯泡的使用寿命 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
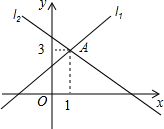 如图直线l1:y=ax+b,与直线l2:y=mx+a交于点A(1,3),那么不等式ax+b<mx+n的解集是( )
如图直线l1:y=ax+b,与直线l2:y=mx+a交于点A(1,3),那么不等式ax+b<mx+n的解集是( )| A. | x>3 | B. | x<3 | C. | x>1 | D. | x<1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
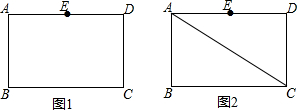
 在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AE平分∠CAB交CD于点F,交CB于点E,过点E作EH∥AB,交BC于H.
在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AE平分∠CAB交CD于点F,交CB于点E,过点E作EH∥AB,交BC于H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com