练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，△ABC中，∠C=90°，sinA=
    1
    3
    ，AC=2，求AB，BC的长．
    考点：解直角三角形
    专题：计算题
    分析：在直角三角形ABC中，由锐角三角函数定义表示出sinA，得到AB=3BC，利用勾股定理求出BC的长，即可确定出AB的长．
    解答：解：∵△ABC中，∠C=90°，sinA=
    1
    3
    ，AC=2，
    ∴
    BC
    AB
    =
    1
    3
    ，即AB=3BC，
    由勾股定理得：AB2=AC2+BC2，即9BC2=4+BC2，
    解得：BC=
    		2
    2
    ，
    则AB=
    3
    		2
    2
    ，BC=
    		2
    2
    ．
    点评：此题考查了解直角三角形，涉及的知识有：勾股定理，以及锐角三角函数定义，熟练掌握勾股定理是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

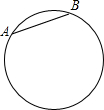    如图是挂在墙上的一面大镜子，上面有两点A、B．小明想知道A、B两点之间的距离，但镜子挂得太高，他只能够到镜子的一部分，无法直接测量，旁边又没有梯子，只有一根长度比圆的直径稍长点的竹竿和一把尺子，你能帮助小明完成吗？若能，请写出测量步骤，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在Rt△ABC中，∠BAC=90°，AD⊥BC于D，BF平分∠ABC交AD于E，交AC于F，FG⊥AD于G，求证：AB=BD+FG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在同一平面内，有直线a1，a2，a3，a4，…，a100，若a1⊥a2，a2∥a3，a3⊥a4，a4∥a5，…，按此规律下去，则a1与a100的位置关系是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知抛物线y=x2+（2k+1）x-k2+k
    （1）求证：此抛物线与x轴有两个不同的交点．
    （2）当k=-1时，求此抛物线与x轴的交点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程组：
    （1）
    5x-6y=9
    7x-4y=-5
                                 
    （2）
    y+1
    4
    =
    x+2
    3
    2x-3y=1
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    新学期，两摞规格相同的数学课本整齐的叠放在讲台上，请根据图中所给出的数据信息，解答下列问题：
    （1）每本书的高度为
     
    cm，课桌的高度为
     
    cm；
    （2）当课本数为x（本）时，请写出同样叠放在桌面上的一摞数学课本高出地面的距离（用含x的代数式表示）；
    （3）桌面上有56本与题（1）中相同的数学课本，整齐叠放成一摞，若从中取走14本，求余下的数学课本高出地面的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    关于x的方程3x+a=0的解与方程2x-4=0的解相同，则a=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△ABC为等腰直角三角形，∠BAC=90°，E、F是BC上的点，且∠EAF=45°，试探究BE2、CF2、EF2间的关系，并说明理由．

    查看答案和解析>>

    同步练习册答案