练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．（1）计算：$\sqrt{4}$+（-2010）0
    （2）解分式方程：$\frac{1}{x-2}$=$\frac{3}{x}$．

    分析 （1）直接利用二次根式以及零指数幂的性质化简，进而求出答案；
    （2）直接利用比例的性质将原式变形，进而解方程即可．

    解答 解：（1）原式=2+1
    =3；

    （2）原式可变形为：
    x=3（x-2），
    x=3x-6，
    x-3x=-6，
    -2x=-6，
    解得：x=3，
    经检验，x=3是原方程的解．

    点评 此题主要考查了实数运算以及分式方程的解法，正确将原式变形去分母是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    15．已知关于x的方程3a+x=$\frac{x}{2}$-5的解为2，a的值是-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．计算：-12+（-$\frac{1}{2}$）-2+（$\sqrt{3}$-π）0+2cos30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图，a∥b，∠1=∠2，∠3=40°，则∠4等于70°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

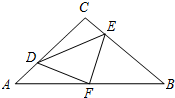    20．如图，在等腰Rt△ABC中，∠C=90°，AC=8，F是AB边上的中点，点D、E分别在AC、BC边上运动，且保持AD=CE．连接DE、DF、EF．在此运动变化的过程中，下列结论：
    ①△DFE是等腰直角三角形；
    ②四边形CDFE的面积保持不变；
    ③△CDE面积的最大值为8；
    ④四边形CDFE不可能为正方形；
    ⑤DE长度的最小值为4．
    其中正确的结论是（填序号）???①②③．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：$\sqrt{2}×\sqrt{\frac{1}{2}}-3\sqrt{2}+\sqrt{8}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

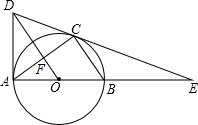    17．如图，AB为⊙O的直径，点C在⊙O上，连接BC、AC，作OD∥BC，与过点A的切线交于点D，连接DC并延长交AB的延长线于点E．
    （1）求证：DE为⊙O的切线．
    （2）若BE=6，cos∠ABC=$\frac{\sqrt{3}}{3}$，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．计算：$|{-3}|+{（\frac{1}{3}）^{-1}}-{（π-1）^0}+\sqrt{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

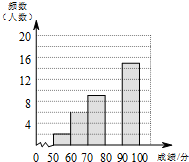    15．为了传承中华优秀传统文化，某校组织了一次八年级350名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中若干名学生的成绩作为样本进行整理，得到下列不完整的统计图表：
    成绩x/分频数频率
    50≤x＜6020.04
    60≤x＜7060.12
    70≤x＜809b
    80≤x＜90a0.36
    90≤x≤100150.30
    请根据所给信息，解答下列问题：
    （1）a=18，b=0.18；
    （2）请补全频数分布直方图；
    （3）这次比赛成绩的中位数会落在80≤x＜90分数段；
    （4）若成绩在90分以上（包括90分）的为“优”等，则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人？

    查看答案和解析>>

    同步练习册答案