
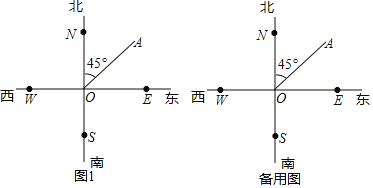
【题目】如图,射线ON,OE、OS、OW分别表示从点O出发的北、东、南、西四个方向,且点A在点O的北偏东45°方向上,点B在点O的北偏西30°方向上.
(1)画出射线OB,若∠BOC与∠AOB互余,请在图中画出∠BOC;
(2)若OP是∠AOC的角平分线,请直接写出AOP的度数.(不需要写计算过程)
科目:初中数学 来源: 题型:
【题目】如图①所示,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D,E,F,G,已知∠CGD=42°
(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示,点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图是用4个全等的长方形拼成的一个“回形”正方形,图中阴影部分面积用2种方法表示可得一个等式,这个等式为_______.
(2)若(4x﹣y)2=9,(4x+y)2=169,求xy的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上的一点,点E在BC边上,连接AE,DE,DC,AE=CD.
(1)求证:△ABE≌△CBD;
(2)若∠BAE=15°,求∠EDC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD,EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.

解:∵∠1+∠2=180°(已知),
∠1+∠EFD=180°(邻补角定义),
∴∠2=∠EFD( )
∴AB∥EF(内错角相等,两直线平行)
∴∠ADE=∠3( )
∵∠3=∠B(已知)
∴∠ADE=∠B( )
∴ (同位角相等,两直线平行)
∴∠AED=∠C(两直线平行,同位角相等).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com