
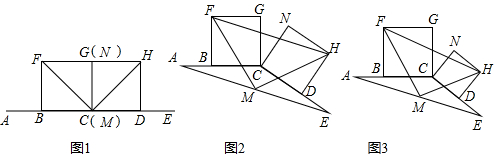
在图1至图3中,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和CDHN都是正方形.AE的中点是M.

1.如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,
求证:FM = MH,FM⊥MH
2.将图-1中的CE绕点C顺时针旋转一个锐角,得到图2,
求证:△FMH是等腰直角三角形
3.将图2中的CE缩短到图3的情况,△FMH还是等腰直角三角形吗?(不必
说明理由)
1.证明:∵四边形BCGF和CDHN都是正方形,
又∵点N与点G重合,点M与点C重合,
∴FB = BM = MG = MD = DH,∠FBM =∠MDH = 90°.
∴△FBM ≌ △MDH.
∴FM = MH.
∵∠FMB =∠DMH = 45°,∴∠FMH = 90°.∴FM⊥HM.
2.证明:连接MB、MD,如图2,设FM与AC交于点P.
∵B、D、M分别是AC、CE、AE的中点,
∴MD∥BC,且MD = BC = BF;MB∥CD,
且MB=CD=DH.
∴四边形BCDM是平行四边形.
∴ ∠CBM =∠CDM.
又∵∠FBP =∠HDC,∴∠FBM =∠MDH.
∴△FBM ≌ △MDH.
∴FM = MH,
且∠MFB =∠HMD.
∴∠FMH =∠FMD-∠HMD =∠APM-∠MFB =∠FBP = 90°.
∴△FMH是等腰直角三角形
3.是
【解析】略


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,小明将一张长方形纸片沿对角线剪开,得到两张三角形纸片(如图2)量得它们的斜边长为10cm,较小锐角为30°再将这两张三角形纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示).
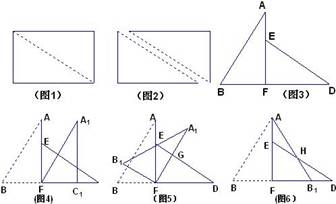
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮忙解决.
1.(1)将图3中的△ABC沿BD向右平移到图4的位置,使点B与点F重合,请你求出平移的距离;
2.(2)将图3中的△ABC绕点F顺时针方向旋转30°到图5的位置,A1F交DE于G,若DG=kEG,求k的值;
3.(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH=DH.
查看答案和解析>>
科目:初中数学 来源:2011年重庆市石柱县九年级期末考试数学卷 题型:解答题
如图1,小明将一张长方形纸片沿对角线剪开,得到两张三角形纸片(如图2)量得它们的斜边长为10cm,较小锐角为30°再将这两张三角形纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示).

小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮忙解决.
1.(1)将图3中的△ABC沿BD向右平移到图4的位置,使点B与点F重合,请你求出平移的距离;
2.(2)将图3中的△ABC绕点F顺时针方向旋转30°到图5的位置,A1F交DE于G,若DG=kEG,求k的值;
3.(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH=DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图(1),小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图(2)),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图(3)的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图(3)至图(6)中统一用F表示)
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决。
(1)将图(3)中△ABF沿BD向右平移到图(4)的位置,使点B与点F重合,请你求出平移的距离;
(2)将图(3)中△ABF绕点F顺时针方向旋转30°到图(5)的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图(3)中的△ABF沿直线AF翻折到图(6)的位置,AB1交DE丁点H,请证明:AH=DH。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com