
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+ ![]() 与y轴相交于点A,点B与点O关于点A对称.
与y轴相交于点A,点B与点O关于点A对称.
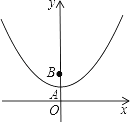
(1)填空:点B的坐标为________;
(2)过点B的直线y=kx+b(其中k<0)与x轴相交于点C,过点C作直线l平行于y轴,P是直线l上一点,且PB=PC,求线段PB的长(用含k的式子表示),并判断点P是否在抛物线上,说明理由.
【答案】(1)(0, ![]() );(2)PB=
);(2)PB=![]() +
+![]() ,点P在抛物线上
,点P在抛物线上
【解析】
(1)由抛物线解析式可求得A点坐标,再利用对称可求得B点坐标;
(2)可先用k表示出C点坐标,过B作BD⊥l于点D,条件可知P点在x轴上方,设P点纵坐标为y,可表示出PD、PB的长.在Rt△PBD中,利用勾股定理可求得y,则可求出PB的长,此时可得出P点坐标,代入抛物线解析式可判断P点在抛物线上.
(1)∵y=﹣x2+![]() 的顶点A的坐标为(0,
的顶点A的坐标为(0,![]() ),∴原点O关于点A的对称点B的坐标为(0,
),∴原点O关于点A的对称点B的坐标为(0,![]() ).
).
故答案为:(0,![]() );
);
(2)∵B点坐标为(0,![]() ),∴直线解析式为y=kx+
),∴直线解析式为y=kx+![]() ,解得:x=﹣
,解得:x=﹣![]() ,∴OC=﹣
,∴OC=﹣![]() .
.
∵PB=PC,∴点P只能在x轴上方,如图,过点B作BD⊥l于点D,设PB=PC=m,则BD=OC=﹣![]() ,CD=OB=
,CD=OB=![]() ,∴PD=PC﹣CD=m﹣
,∴PD=PC﹣CD=m﹣![]() .
.
在Rt△PBD中,由勾股定理可得:PB2=PD2+BD2,即m2=(m﹣![]() )2+(﹣
)2+(﹣![]() )2,解得:m=
)2,解得:m=![]() +
+![]() ,∴PB=
,∴PB=![]() +
+![]() ,∴点P坐标为(﹣
,∴点P坐标为(﹣![]() +
+![]() ).
).
当x=﹣![]() 时,代入抛物线解析式可得:y=
时,代入抛物线解析式可得:y=![]() +
+![]() ,∴点P在抛物线上.
,∴点P在抛物线上.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中AC=BC,∠ACB=90°,以BC为直径作⊙O,连接OA,交⊙O于点D,过D点作⊙O的切线交AC于点E,连接B、D并延长交AC于点F.则下列结论错误的是( )
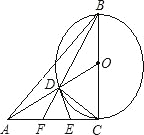
A. △ADE∽△ACO B. △AOC∽△BFC
C. △DEF∽△DOC D. CD2=DFDB
查看答案和解析>>
科目:初中数学 来源: 题型:
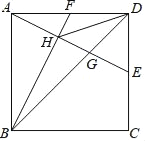
【题目】已知:正方形ABCD中,AB=4,E为CD边中点,F为AD边中点,AE交BD于G,交BF于H,连接DH.
(1)求证:BG=2DG;
(2)求AH:HG:GE的值;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
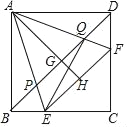
【题目】如图,正方形ABCD的边长为10,点E、F分别在边BC、CD上,且∠EAF=45°,AH⊥EF于点H,AH=10,连接BD,分别交AE、AH、AF于点P、G、Q.
(1)求△CEF的周长;
(2)若E是BC的中点,求证:CF=2DF;
(3)连接QE,求证:AQ=EQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 是
是![]() 轴上的一个动点,设
轴上的一个动点,设![]() .
.
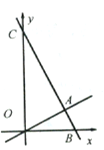
(1)若![]() 的值最小,求
的值最小,求![]() 的值;
的值;
(2)若直线![]() 将
将![]() 分割成两个等腰三角形,请求出
分割成两个等腰三角形,请求出![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
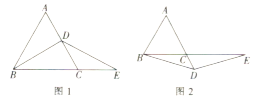
【题目】如图,![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 上的一个动点,
上的一个动点,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)当![]() 是
是![]() 的中点时,求证:
的中点时,求证:![]() .
.
(2)如图1,若点![]() 在边
在边![]() 上,猜想线段
上,猜想线段![]() 与
与![]() 之间的关系,并说明理由.
之间的关系,并说明理由.
(3)如图2,若点![]() 在
在![]() 的延长线上,(1)中的结论是否仍然成立,请说明理由.
的延长线上,(1)中的结论是否仍然成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,若S△ABC=18,设△ADF的面积为S1,△CEF的面积为S2,则S1-S2的值是______.
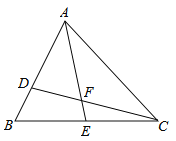
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面宜角坐标系xOy中,直线y=![]() x+4与x轴,y轴交于点A,B.第一象限内有一点P(m,n),正实数m,n满足4m+3n=12
x+4与x轴,y轴交于点A,B.第一象限内有一点P(m,n),正实数m,n满足4m+3n=12
(1)连接AP,PO,△APO的面积能否达到7个平方单位?为什么?
(2)射线AP平分∠BAO时,求代数式5m+n的值;
(3)若点A′与点A关于y轴对称,点C在x轴上,且2∠CBO+∠PA′O=90°,小慧演算后发现△ACP的面积不可能达到7个平方单位.请分析并评价“小薏发现”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在
在![]() 的
的![]() 边上,
边上,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,若添加条件________,则四边形
,若添加条件________,则四边形![]() 是矩形;若添加条件________,则四边形
是矩形;若添加条件________,则四边形![]() 是菱形;若添加条件________,则四边形
是菱形;若添加条件________,则四边形![]() 是正方形.
是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com