
| A.内切 | B.外切 | C.内含 | D.相交 |
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源:不详 题型:解答题
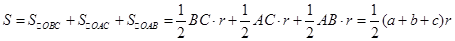 .
.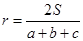 .
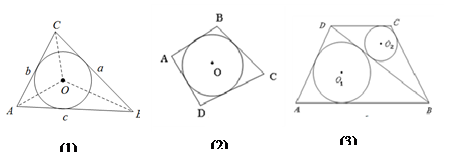
.
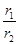 的值.
的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
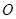 的半径为
的半径为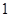 ,正方形
,正方形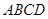 顶点
顶点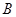 坐标为
坐标为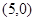 ,顶点
,顶点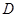 在⊙
在⊙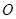 上运动.
上运动.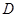 运动到与点
运动到与点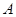 、
、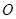 在同一条直线上时,试证明直线
在同一条直线上时,试证明直线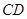 与⊙
与⊙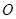 相切;
相切;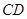 与⊙
与⊙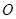 相切时,求
相切时,求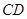 所在直线对应的函数关系式;
所在直线对应的函数关系式;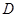 的横坐标为
的横坐标为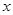 ,正方形
,正方形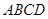 的面积为
的面积为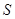 ,求
,求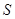 与
与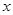 之间的函数关系式,并求出
之间的函数关系式,并求出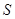 的最大值与最小值.
的最大值与最小值.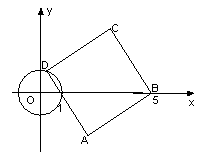
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
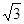 ≈1.7,保留三个有效数字);
≈1.7,保留三个有效数字);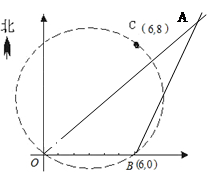
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.相交或相切 | B.相切或相离 | C.相交或内含 | D.相切或内含 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com