
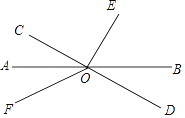
【题目】如图,若直线AB与直线CD交于点O,OA平分∠COF,OE⊥CD.
(1)写出图中与∠EOB互余的角;
(2)若∠AOF=30°,求∠BOE和∠DOF的度数.
【答案】(1)∠COA,∠FOA,∠BOD;(2)60°.
【解析】试题分析:(1)由于OA平分∠COF和∠COA与∠BOD是对顶角,得到∠COA=∠FOA=∠BOD,根据垂直定义有∠EOB+∠BOD=90°,根据互为余角的定义即可得到结论;(2)由(1)知∠COA=∠FOA=∠BOD=30°,由平角的意义可求得∠DOF,根据垂直定义可求得∠BOE.
(1)解:∵OA平分∠COF, ∴∠COA=∠FOA=∠BOD,
∵OE⊥CD,
∴∠EOB+∠BOD=90°,
∴∠COA+∠EOB=90°,∠FOA+∠EOB=90°,
∴与∠EOB互余的角是:∠COA,∠FOA,∠BOD
(2)解:∵∠AOF=30°,由(1)知∠COA=∠FOA=∠BOD=30°, ∴∠DOF=180°﹣∠FOA﹣∠BOD=120°,
∵OE⊥CD,
∴∠BOE=90°﹣30°=60°


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
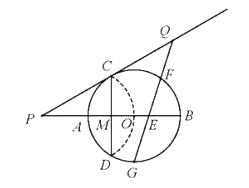
【题目】(2016广东省深圳市第22题)如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,链接PC。
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合)。问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教育工会为庆祝重阳节活动,在九月份组织退休职工到北京长城、故宫五日游,现联系了青年旅行社、教育旅行社,两家旅行社报价均为3000元/人,两家旅行社同时都对10人以上的团体推出了优惠举措:青年旅行社对每位职工七五折优惠;而教育旅行社是免去一位带队领导的费用,其余职工八折优惠.
(1)如果设参加旅游的职工共有m(m>10)人,则甲旅行社的费用为 元,乙旅行社的费用为 元;(用含m的代数式表示,并化简.)
(2)假如这个单位现组织包括带队领导在内的共20名职工到北京旅游,该单位选择哪一家旅行社比较优惠?请说明理由.
(3)如果计划在九月份外出旅游5天,设最中间一天的日期为m,则这5天的日期之和为 .(用含m的代数式表示,并化简.)
(4)假如这五天的日期之和为70,则他们于九月几号出发.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空,并在括号内说明理由: 如图,已知∠BAP与∠APD互补,∠1=∠2,说明∠E=∠F.
证明:∵∠BAP与∠APD互补(_________), ∴AB∥CD(____________),
∴∠BAP=∠APC(__________).
又∵∠1=∠2(__________),
∴∠BAP﹣∠1=∠APC﹣∠2(_________),即∠3=∠4,
∴AE∥PF,(___________),
∴∠E=∠F(__________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com