
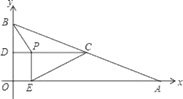
【题目】在平面直角坐标系中,已知点A、B的坐标分别为(10,0)、(0,4),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C以每秒1个单位匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P运动的时间为_____秒.
【答案】1或4
【解析】
先求出CD和PE的长,再判定△EPC∽△PDB,列出相关的比例式,求得DP的长,根据点P的运动速度即可求得运动时间.
解:如图,当BP所在直线与EC所在直线垂直时,设BP与CE交于点F,
∵点A、B的坐标为(10,0)、(0,4),
∴AO=10,BO=4,
∵CD⊥BO,C是AB的中点,
∴CD是△AOB的中位线,
∴BD=DO=![]() BO=2=PE,CD=
BO=2=PE,CD=![]() AO=5,CD∥AO,
AO=5,CD∥AO,
设DP=x,则CP=5-x,
在Rt△PBD和Rt△PCF中,∠BPD=∠CPF,
∴PCE=∠DBP,
∴Rt△BPD∽Rt△CEP,
∴![]() ,
,
∴![]() ,
,
∴x=1或x=4,
∴当x=1时,即DP=1,运动时间为1秒;当x=4时,运动时间为4秒.

故答案为:1或4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,与y轴交于C点,M点在抛物线的对称轴上,当点M到点B的距离与到点C的距离之和最小时,点M的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】情境![]() :小芳离开家去学校上学,走了一段路后,发现自己作业本忘家里了,于是返回家里找到作业本,然后又赶快去学校;
:小芳离开家去学校上学,走了一段路后,发现自己作业本忘家里了,于是返回家里找到作业本,然后又赶快去学校;
情境![]() :小明从家出发去图书馆还书,走了一段路程后,发现时间有点紧张,便以更快的速度前进.
:小明从家出发去图书馆还书,走了一段路程后,发现时间有点紧张,便以更快的速度前进.

(1)情境![]() 所对应的函数图象分别是_______,_______(填写序号);
所对应的函数图象分别是_______,_______(填写序号);
(2)请你为剩下的函数图象写出一个适合的情景.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列问题:
(1)阅读理解:
如图1,在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.
的取值范围.
解决此问题可以用如下方法:延长![]() 到点
到点![]() 使
使![]() ,再连接
,再连接![]() (或将
(或将![]() 绕着
绕着![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,把
,把![]() 、
、![]() ,
,![]() 集中在
集中在![]() 中,利用三角形三边的关系即可判断.中线
中,利用三角形三边的关系即可判断.中线![]() 的取值范围是______.
的取值范围是______.
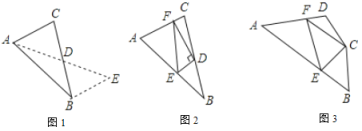
(2)问题解决:
如图2,在![]() 中,
中,![]() 是
是![]() 边上的中点,
边上的中点,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
(3)问题拓展:
如图3,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点作一个
为顶点作一个![]() 角,角的两边分别交
角,角的两边分别交![]() ,
,![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ,探索线段
,探索线段![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=6,BC=8,若AC,BC边上的中线BE,AD 垂直相交于点O,则AB=( )

A. 5 B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
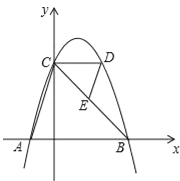
【题目】如图,抛物线y=﹣(x﹣1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线于另一点D,连结AC,DE∥AC交边CB于点E.
(1)求A,B两点的坐标;
(2)求△CDE与△BAC的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
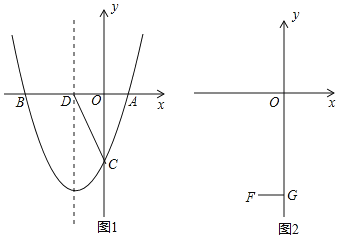
【题目】抛物线y=x2+bx+c与x轴交于A(1,0),B(m,0),与y轴交于C.
(1)若m=-3,求抛物线的解析式,并写出抛物线的对称轴;
(2)如图1,在(1)的条件下,设抛物线的对称轴交x轴于D,在抛物线对称轴左侧上有 一点E,使S△ACE=S△ACD,求E点的坐标;
(3) 如图2,设F(-1,-4),FG⊥y轴于G,在线段OG上是否存在点P,使 ∠OBP=∠FPG? 若存在,求m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
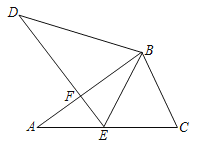
【题目】如图,已知∠A=∠D,AB=DB,点E在AC边上,∠AED=∠CBE,AB和DE相交于点F.
(1)求证:△ABC≌△DBE.
(2)若∠CBE=50°,求∠BED的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com