
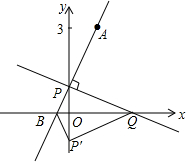
 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b≠0).直线AP交x轴于点B,记点P关于x轴的对称点为P′,点Q为x轴上一动点.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b≠0).直线AP交x轴于点B,记点P关于x轴的对称点为P′,点Q为x轴上一动点.分析 (1)根据b的值表示出直线AP解析式,把A坐标代入求出k的值,确定出AP解析式,进而得出B坐标,确定出OB的长;
(2)设出AP解析式为y=kx+b,把A坐标代入表示出k,即可表示出OB的长;
(3)存在四边形PBP′Q,使四边形PBP′Q为正方形,若四边形PBP′Q为正方形,则有OB=OP=OP′=OQ,列出关于b的方程,求出方程的解得到b的值,即可确定出Q坐标.
解答 解:(1)由b=1,得到P(0,1),
设直线AP解析式为y=kx+1,
把A(1,3)代入得:3=k+1,
解得:k=2,
∴直线OP解析式为y=2x+1,
令y=0,得到x=-$\frac{1}{2}$,
∴B(-$\frac{1}{2}$,0),即OB=$\frac{1}{2}$;
(2)根据题意得:直线AP解析式为y=kx+b,
把(1,3)代入得:3=k+b,即k=3-b,
∴直线解析式为y=(3-b)x+b,
令y=0,得到x=$\frac{b}{b-3}$,即OB=-$\frac{b}{b-3}$;
(3)存在四边形PBP′Q,使四边形PBP′Q为正方形,理由为:
若四边形PBP′Q为正方形,则有OB=OP=OP′=OQ,即-$\frac{b}{b-3}$=b,
解得:b=2,
则b=2,Q(2,0).
点评 此题属于一次函数综合题,涉及的知识有:待定系数法确定一次函数解析式,坐标与图形性质,正方形的性质,以及一次函数的性质,熟练掌握待定系数法是解本题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
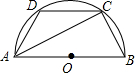 如图,AB是半圆O的直径,D是$\widehat{AC}$上一点,若∠BAC=35°,则∠ADC的度数是( )
如图,AB是半圆O的直径,D是$\widehat{AC}$上一点,若∠BAC=35°,则∠ADC的度数是( )| A. | 100° | B. | 120° | C. | 125° | D. | 130° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:| 类别 | 人数 | 占总人数比例 |
| 重视 | a | b |
| 一般 | 57 | 0.285 |
| 不重视 | c | 0.36 |
| 说不清楚 | 9 | 0.045 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | 6 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com