
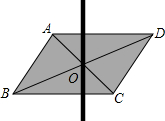
 用硬纸板剪一个平行四边形,做出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处.若木条与AD交于点E、与BC交于点F,拨动细木条
用硬纸板剪一个平行四边形,做出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处.若木条与AD交于点E、与BC交于点F,拨动细木条分析 (1)由四边形ABCD是平行四边形,可得AD∥BC,OA=OC,继而证得△AOE≌△COF(ASA),则可证得结论;
(2)根据平行四边形的判定和等腰梯形的判定解答即可;
(3)根据菱形的判定解答即可.
解答 解:(1)OE=OF.
理由:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠OAE=∠OCF,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠AOE=∠COF}\\{OA=OC}\\{∠OAE=∠OCF}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴OE=OF;
(2)当EF∥AB时,四边形ABFE为平行四边形;
∵AE∥BF,EF∥AB,
∴四边形ABFE为平行四边形;
当EF=AB时,四边形ABFE为等腰梯形;
∵AE∥BF,EF=AB,
∴四边形ABFE为等腰梯形;
(3)当AB=BF时,四边形ABFE为菱形;
∵AE∥BF,AE=BF,AB=BF,
∴四边形ABFE为菱形.
点评 此题考查了平行四边形的性质以及全等三角形的判定与性质.注意证得△AOE≌△COF是解此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.1010010001 | B. | $\sqrt{9}$ | C. | $\root{3}{-64}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com