
【题目】如图,直线AB,CD相交于点O,OE⊥AB于点O,OF⊥CD于点O,下列结论:
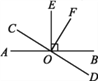
①∠EOF的余角有∠EOC和∠BOF;
②∠EOF=∠AOC=∠BOD;
③∠AOC与∠BOF互为余角;
④∠EOF与∠AOD互为补角.其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
科目:初中数学 来源: 题型:
【题目】菱形ABCD的一条对角线长为6,边AB的长是方程x2﹣7x+12=0的一个根,则菱形ABCD的周长为( )
A. 16 B. 12 C. 16或12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
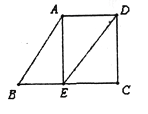
【题目】如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.
(1)求∠AED的度数;
(2)当∠EDC满足什么条件时,AE∥DC,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
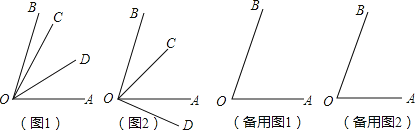
【题目】【问题提出】已知∠AOB=70°,∠AOD=![]() ∠AOC,∠BOD=3∠BOC(∠BOC<45°),求∠BOC的度数.
∠AOC,∠BOD=3∠BOC(∠BOC<45°),求∠BOC的度数.
【问题思考】聪明的小明用分类讨论的方法解决.
(1)当射线OC在∠AOB的内部时,①若射线OD在∠AOC内部,如图1,可求∠BOC的度数,解答过程如下:
设∠BOC=α,∴∠BOD=3∠BOC=3α,∴∠COD=∠BOD﹣∠BOC=2α,∴∠AOD=![]() ∠AOC,
∠AOC,
∴∠AOD=∠COD=2α,∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,∴α=14°,∴∠BOC=14°
问:当射线OC在∠AOB的内部时,②若射线OD在∠AOB外部,如图2,请你求出∠BOC的度数;
【问题延伸】(2)当射线OC在∠AOB的外部时,请你画出图形,并求∠BOC的度数.
【问题解决】综上所述:∠BOC的度数分别是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE=__________度.

(第22题)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com