
如图,抛物线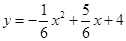 与直线
与直线 交于点A 、B,与y轴交于点C.
交于点A 、B,与y轴交于点C.
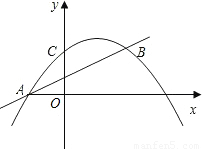
(1)求点A、B的坐标;
(2)若点P是直线x=1上一点,是否存在△PAB是等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
符合条件的点P共有4个,分别为:P1(1,-8),P1′(1,8),P2(1,-4),P2′(1,12).
【解析】
试题分析:(1)将两个函数解析式联立,组成一个方程组求得x、y的值即可得到两点的坐标;
(2)存在符合条件的点P共有3个.因而分三类情形探求.
①以AB为腰且顶角为∠A:△P1AB;②以AB为腰且顶角为∠B:△P2AB;③以AB为底,顶角为∠P的△PAB有1个,即△P3AB.综上得出符合条件的点.
试题解析:
解:(1)由题意得: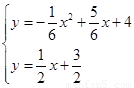 解得:
解得: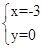 或
或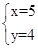
∴A(-3,0)B(5,4)
(2)存在符合条件的点P共有4个.以下分三类情形探求.
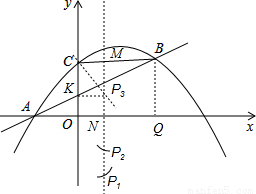
由A(-3,0),B(5,4),C(0,4),可得BC∥x轴,BC=AC,
设直线x=1与x轴交于N,与CB交于M,
过点B作BQ⊥x轴于Q,易得BQ=4,AQ=8,AN=4,BM=4,
①以AB为腰且顶角为∠A:△P1AB.
∴AB2=AQ2+BQ2=82+42=80,
在Rt△ANP1中,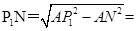
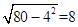 ,
,
∴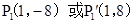 ,
,
②以AB为腰且顶角为∠B:△P2AB.
在Rt△BMP2中, 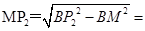
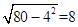 ,
,
∴P2(1,-4)或P2′(1,12),
③以AB为底,顶角为∠P的△PAB有1个,即△P3AB.
画AB的垂直平分线交抛物线对称轴于P3,此时平分线必过等腰△ABC的顶点C.
过点P3作P3K垂直y轴,垂足为K,显然Rt△P3CK∽Rt△BAQ.
∴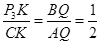 .
.
∵P3K=1,
∴CK=2,于是OK=2,
∴P3(1,2),
而P3(1,2)在线段AB上,构不成三角形,舍去.
综上,符合条件的点P共有4个,分别为: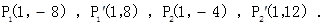
考点:二次函数综合题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
 =-1,与x轴交于点C,且∠ABC=90°
=-1,与x轴交于点C,且∠ABC=90°查看答案和解析>>
科目:初中数学 来源:2013-2014学年安徽蚌埠六中九年级11月阶段检测数学试卷(解析版) 题型:解答题
如图,抛物线 与直线
与直线 交于C,D两点,其中点C在y轴上,点D的坐标为
交于C,D两点,其中点C在y轴上,点D的坐标为 。点P是y轴右侧的抛物线上一动点,过点P作
。点P是y轴右侧的抛物线上一动点,过点P作 轴于点E,交CD于点F.
轴于点E,交CD于点F.

(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O,C,P,F为顶点的四边形是平行四边形?请说明理由。
(3)若存在点P,使 ,请直接写出相应的点P的坐标
,请直接写出相应的点P的坐标
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(河南卷)数学(解析版) 题型:解答题
如图,抛物线 与直线
与直线 交于C,D两点,其中点C在y轴上,点D的坐标为
交于C,D两点,其中点C在y轴上,点D的坐标为 。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
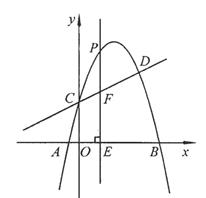
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O,C,P,F为顶点的四边形是平行四边形?请说明理由;
(3)若存在点P,使∠PCF=450,请直接写出相应的点P的坐标。
查看答案和解析>>
科目:初中数学 来源:2011-2012年北京师大附中九年级第一学期期中考试数学卷 题型:解答题
已知:如图,抛物线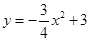 与
与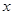 轴交于点
轴交于点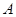 ,点
,点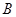 ,与直线
,与直线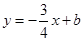 相交于点
相交于点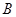 ,点
,点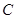 ,直线
,直线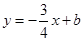 与
与 轴交于点
轴交于点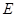 .
.
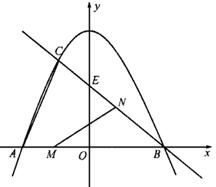
1.(1)求 的面积.
的面积.
2.(2)若点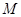 在线段
在线段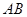 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从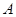 向
向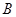 运动(不与
运动(不与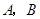 重合),同时,点
重合),同时,点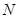 在射线
在射线 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从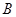 向
向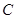 运动.设运动时间为
运动.设运动时间为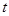 秒,请写出
秒,请写出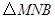 的面积
的面积 与
与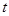 的函数关系式,并求出点
的函数关系式,并求出点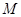 运动多少时间时,
运动多少时间时,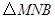 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com