
【题目】如图,在△ABC中,∠ABC的平分线BE与∠ACB外角的平分线CE交于点E.
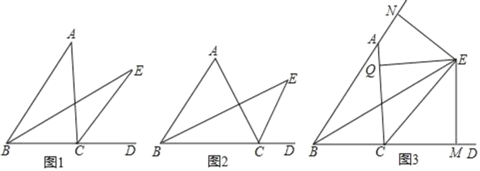
(1)如图1,若∠BAC=40°,则∠BEC= °
(2)如图2,将∠BAC变为60°,则∠BEC= °,写出∠BAC与∠BEC的关系;并说明你的理由
(3)在图1的基础上过点E分别作EN⊥BA于N,EQ⊥AC于Q,EM⊥BD于M,如图3,
求证:△ANE≌AQE,并求出∠NAE的度数.
【答案】(1)20°;(2)30°, ∠E=![]() ∠A,理由见解析;(3)见解析,∠NAE=70°.
∠A,理由见解析;(3)见解析,∠NAE=70°.
【解析】
(1)证明∠E=![]() ∠A,即可解决问题;
∠A,即可解决问题;
(2)利用(1)中结论解决问题即可;
(3)连接AE.证明Rt△ANE≌Rt△AQE(HL)即可解决问题;
(1)依据三角形外角性质∠A=∠ACD∠ABC,∠E=∠ECD∠EBD
∵∠ABC的平分线与∠ACB外角的平分线交于点E,
∴∠EBD=![]() ∠ABC,∠ECD=
∠ABC,∠ECD=![]() ∠ACD
∠ACD
∴∠E=∠ECD∠EBD=![]() ∠ACD
∠ACD![]() ∠ABC=
∠ABC=![]() ∠A=20°.
∠A=20°.
(2)30°,∠E=![]() ∠A
∠A
理由:∠A=∠ACD﹣∠ABC,∠E=∠ECD﹣∠EBD
∵∠ABC的平分线与∠ACB外角的平分线交于点E,
∴∠EBD=![]() ∠ABC,∠ECD=
∠ABC,∠ECD=![]() ∠ACD
∠ACD
∴∠E=∠ECD﹣∠EBD=![]() ∠ACD﹣
∠ACD﹣![]() ∠ABC=
∠ABC=![]() ∠A
∠A
(3)连接AE.
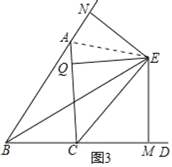
∵CE平分∠ACD,EQ⊥AC,EM⊥BD,
∴EQ=EM,
同理EN=EM
∴EN=EQ,
在Rt△ANE和Rt△AQE中,
![]() ,
,
∴Rt△ANE≌Rt△AQE(HL),
∴∠EAQ=∠EAN,
∵∠BAC=40°,
∴∠NAQ=140°,
∴∠NAE=![]() ×140°=70°
×140°=70°


科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤![]() PD=EC.其中有正确有( )个.
PD=EC.其中有正确有( )个.

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从-2,-1,1,2这四个数中,任取两个不同的数作为一次函数y=kx+b的系数k,b,则一次函数y=kx+b的图象不经过第四象限的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 的顶点
的顶点![]() 为坐标原点,顶点
为坐标原点,顶点![]() 在
在![]() 轴正半轴上,顶点
轴正半轴上,顶点![]() 、
、![]() 在第一象限,
在第一象限,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,将四边形
上,将四边形![]() 沿直线
沿直线![]() 翻折,使点
翻折,使点![]() 和点
和点![]() 分别落在这个坐标平面内的
分别落在这个坐标平面内的![]() 和
和![]() 处,且
处,且![]() ,某正比例函数图象经过
,某正比例函数图象经过![]() ,则这个正比例函数的解析式为( )
,则这个正比例函数的解析式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农产品店利用网络将优质土特产销往全国,其中销售的核桃和花生这两种商品的相关信息如下表:
商品 | 核桃 | 花生 |
规格 | 1 kg/袋 | 2 kg/袋 |
利润 | 10元/袋 | 8元/袋 |
根据上表提供的信息,解答下列问题:
(1)已知今年上半年,该店销售上表规格的核桃和花生共3000kg,获得利润21000元,求上半年该店销售这种规格的核桃和花生各多少袋;
(2)根据之前的销售情况,估计今年下半年,该店还能销售上表规格的核桃和花生共2000kg,其中,核桃的销售量不低于600kg.假设今年下半年,销售上表规格的核桃为![]() (kg),销售上表规格的核桃和花生获得的总利润为
(kg),销售上表规格的核桃和花生获得的总利润为![]() (元),写出
(元),写出![]() 与
与![]() 之间的函数关系式,并求下半年该店销售这种规格的核桃和花生至少获得的总利润.
之间的函数关系式,并求下半年该店销售这种规格的核桃和花生至少获得的总利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图1:已知直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,以
两点,以![]() 为直角顶点在第一象限内做等腰Rt△
为直角顶点在第一象限内做等腰Rt△![]() .
.

(1)求![]() ,
,![]() 两点的坐标;
两点的坐标;
(2)求![]() 所在直线的函数关系式;
所在直线的函数关系式;
(3)如图2,直线![]() 交
交![]() 轴于点
轴于点![]() ,在直线
,在直线![]() 上取一点
上取一点![]() ,使
,使![]() ,
,![]() 与
与![]() 轴相交于点
轴相交于点![]() .
.
①求证:![]() ;
;
②在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使△
,使△![]() 的面积等于△
的面积等于△![]() 的面积?若存在,直接写出点
的面积?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△A1B1C1,△A2B2C2的周长相等,现有两个判断:
①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;
②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,
对于上述的两个判断,下列说法正确的是( )
A. ①正确,②错误 B. ①错误,②正确 C. ①,②都错误 D. ①,②都正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com