
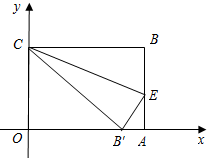
 已知如图,在直角坐标系中放入一个边长OA为8的长方形纸片ABCO.
已知如图,在直角坐标系中放入一个边长OA为8的长方形纸片ABCO.分析 (1)根据题意直接利用HL定理得出:△CBE≌△CB′E;
(2)利用OA=8进而得出A点坐标;
(3)首先表示出OB′,AB′的长进而利用三角形面积得出答案.
解答 (1)证明:∵∠EBC=∠EB′C=90°,
∴△△CBE和△CB′E都是直角三角形,
在Rt△CBE和Rt△CB′E中
$\left\{\begin{array}{l}{EC=EC}\\{BE=B′E}\end{array}\right.$,
∴Rt△CBE≌Rt△CB′E(HL);
(2)解:∵边长OA为8,
∴A点的坐标为:(8,0);
(3)解:∵AE=2,OC=x,
∴BE=B′E=x-2,
∴AB′=$\sqrt{{(x-2)^{2}-2}^{2}}$=$\sqrt{{x}^{2}-4x}$,
则OB′=8-$\sqrt{{x}^{2}-4x}$,
∴△OC B′与△AE B′的面积的和为:
y=$\frac{1}{2}$x(8-$\sqrt{{x}^{2}-4x}$)+$\frac{1}{2}$$\sqrt{{x}^{2}-4x}$×2
=4x-($\frac{1}{2}$x-1)$\sqrt{{x}^{2}-4x}$.
点评 此题主要考查了全等三角形的判定以及点的坐标性质和勾股定理等知识,表示出OB′,AB′的长是解题关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
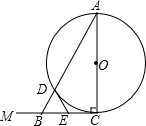 如图1,已知∠ACM=90°,且AC=2,以AC为直径作⊙O,B是射线CM上的一动点,以1个单位/秒,从点C向CM方向运动,运动时间为t秒,连结AB交⊙O 于另一点D,BC的中点为E,
如图1,已知∠ACM=90°,且AC=2,以AC为直径作⊙O,B是射线CM上的一动点,以1个单位/秒,从点C向CM方向运动,运动时间为t秒,连结AB交⊙O 于另一点D,BC的中点为E,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
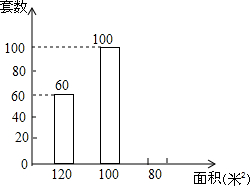 某房地产开发商开发了套内面积分别为“120米2”、“100米2”、“80米2”三种房源其200套,售房部将每种房源套数及每平方的价格绘制了表格和直方图如下:
某房地产开发商开发了套内面积分别为“120米2”、“100米2”、“80米2”三种房源其200套,售房部将每种房源套数及每平方的价格绘制了表格和直方图如下:| 房源类型 | 套内售价(元/米2) |
| 120米2 | 10000 |
| 100米2 | 8000 |
| 80米2 | 4750 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com