
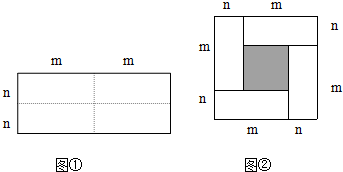
���� ��1������ͼ���и������ֵ�����ó����ɣ�
��2�����ݣ�1���еĽ�����ɵó��𰸣�
��3���ȸ��ݣ�2���Ľ�����б��Σ��ٴ���������ɣ�
��� �⣺��1��ͼ����Ӱ���ֵ����Ϊ��m-n��2��m+n��2-4mn��
�ʴ�Ϊ����m-n��2����m+n��2-4mn��
��2����a-b��2=��a+b��2-4ab��
�ʴ�Ϊ����a-b��2=��a+b��2-4ab��
��3����a+b=7��ab=-5��
�ࣨa-b��2=��a+b��2-4ab=72-4����-5��=69��
���� ���⿼������ȫƽ����ʽ��Ӧ�ã��������ȫƽ����ʽ�ǽ����Ĺؼ���ע�⣺��a+b��2=a2+2ab+b2����a-b��2=a2-2ab+b2����a-b��2=��a+b��2-4ab��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
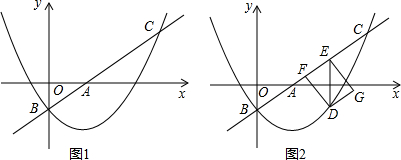
 ��ͼ����֪�߶�AB=4��OΪAB���е㣬P��ƽ���ڵ�-�����㣬���˶������б���OP=1���䣬����BP����PB�Ƶ�P��ʱ����ת90�㵽PC������BC��AC�����߶�AC����ȡֵ��Χ��$\sqrt{2}$��AC��3$\sqrt{2}$��
��ͼ����֪�߶�AB=4��OΪAB���е㣬P��ƽ���ڵ�-�����㣬���˶������б���OP=1���䣬����BP����PB�Ƶ�P��ʱ����ת90�㵽PC������BC��AC�����߶�AC����ȡֵ��Χ��$\sqrt{2}$��AC��3$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С����Сӱ��ס��ͬһ����վ�ڵ�ͬһС���ڣ����������˸���ȥ������������飮Сӱ�˵�����С���ɰְֿ�˽�ҳ�ǰ������֪�ö�˽�ҳ���ʻ��·�ߺ͵���·��ǡ����ͬһֱ���ϣ���˽�ҳ����ٶȱȵ���������������ͬʱ��������������ʱ��Ϊt���ӣ�С����Сӱ֮��ľ���ΪS��S��t�IJ��ֺ���ͼ����ͼ��ʾ��
С����Сӱ��ס��ͬһ����վ�ڵ�ͬһС���ڣ����������˸���ȥ������������飮Сӱ�˵�����С���ɰְֿ�˽�ҳ�ǰ������֪�ö�˽�ҳ���ʻ��·�ߺ͵���·��ǡ����ͬһֱ���ϣ���˽�ҳ����ٶȱȵ���������������ͬʱ��������������ʱ��Ϊt���ӣ�С����Сӱ֮��ľ���ΪS��S��t�IJ��ֺ���ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
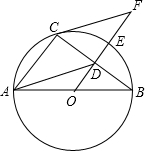 ��ͼ��ABΪԲO��ֱ������C��E��Բ�ϣ��ҵ�E�ǻ�BC���е㣬OE����BC�ڵ�D����F��OE���ӳ����ϣ��ҡ�BCF=��BAC��BC=8��DE=2��
��ͼ��ABΪԲO��ֱ������C��E��Բ�ϣ��ҵ�E�ǻ�BC���е㣬OE����BC�ڵ�D����F��OE���ӳ����ϣ��ҡ�BCF=��BAC��BC=8��DE=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
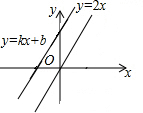 ��ͼ��һ�κ���y=kx+b��ͼ��������������y=2x��ͼ��ƽ���Ҿ����㣨-1��3������b��ֵ��5��
��ͼ��һ�κ���y=kx+b��ͼ��������������y=2x��ͼ��ƽ���Ҿ����㣨-1��3������b��ֵ��5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
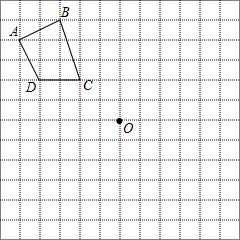 ��ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У������˸���ı���ABCD�������������ߵĽ��㣩���O��
��ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У������˸���ı���ABCD�������������ߵĽ��㣩���O���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������y=ax2-x+c������Q ��-2��4���������Ķ���P�ĺ�����Ϊ-1������������x���ཻ��A��B���㣬
��ͼ����֪������y=ax2-x+c������Q ��-2��4���������Ķ���P�ĺ�����Ϊ-1������������x���ཻ��A��B���㣬�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com