
【题目】俄罗斯世界杯足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每上涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售量为y本,销售单价为x元.
(1)请直接写出y与x之间的函数关系式和自变量x的取值范围;
(2)将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润w元最大?最大利润是多少元?
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,已知点
,已知点![]() 的横坐标为-5,直线
的横坐标为-5,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
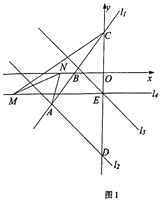
(1)求直线![]() 的解析式;
的解析式;
(2)将直线![]() 向上平移6个单位得到直线
向上平移6个单位得到直线![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,若点
,若点![]() 为垂线
为垂线![]() 上的一个动点,点
上的一个动点,点![]() 为
为![]() 轴上的一个动点,当
轴上的一个动点,当![]() 的值最小时,求此时点
的值最小时,求此时点![]() 的坐标及
的坐标及![]() 的最小值;
的最小值;
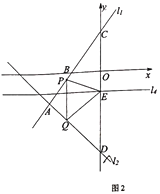
(3)已知点![]() 、
、![]() 分别是直线
分别是直线![]() 、
、![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() 、
、![]() ,是否存在点
,是否存在点![]() 、
、![]() ,使得
,使得![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,若存在,求点
为直角顶点的等腰直角三角形,若存在,求点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
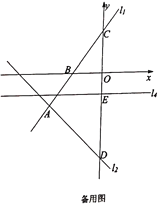
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图.
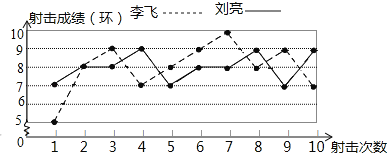
根据图所提供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐( )
A. 李飞或刘亮 B. 李飞 C. 刘亮 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
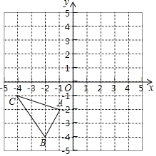
【题目】如图,在平面直角坐标系中,![]() 的三个顶点分别为
的三个顶点分别为![]() ,
,![]() ,
,![]() .
.
![]() 把
把![]() 向上平移
向上平移![]() 个单位后得到
个单位后得到![]() ,请画出
,请画出![]() ;
;
![]() 已知点
已知点![]() 与点
与点![]() 关于直线
关于直线![]() 成轴对称,请画出直线
成轴对称,请画出直线![]() 及
及![]() 关于直线
关于直线![]() 对称的
对称的![]() .
.
![]() 在
在![]() 轴上存在一点
轴上存在一点![]() ,满足点
,满足点![]() 到点
到点![]() 与点
与点![]() 距离之和最小,请直接写出
距离之和最小,请直接写出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县举办老、中、青三个年龄段五公里竞走活动,其人数比为![]() ,如图所示的扇形统计图表示 上述分布情况,已知老人有
,如图所示的扇形统计图表示 上述分布情况,已知老人有![]() 人,则下列说法不正确的是( )
人,则下列说法不正确的是( )
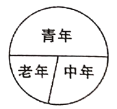
A. 老年所占区域的圆心角是![]() B. 参加活动的总人数是
B. 参加活动的总人数是![]() 人
人
C. 中年人比老年人多![]() D. 老年人比青年人少
D. 老年人比青年人少![]() 人
人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:h),随机调査了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
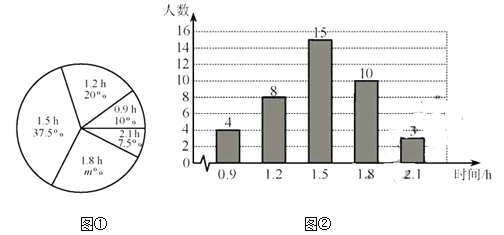
(Ⅰ)本次接受调查的初中学生人数为___________,图①中m的值为_____________;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
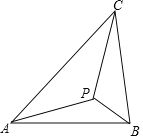
【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
A.5 B.4 C.3+![]() D.2+
D.2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示,直线l经过点(0,1),并且与x轴平行,△A1B1C1与△ABC关于直线l对称.
(1)画出三角形A1B1C1;
(2)若点P(m,n)在AC边上,则点P关于直线l的对称点P1的坐标为 ;
(3)在直线l上画出点Q,使得QA+QC的值最小.
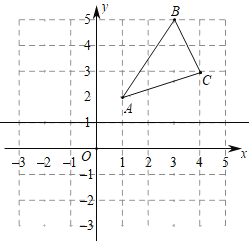
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com