
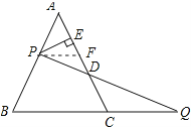
【题目】如图,P是等边△ABC的AB边上一点,过P作PE⊥AC于E,在BC的延长线上截取CQ=AP,连接PQ交AC于点D.
(1)若∠Q=28°,求∠EPD的度数;
(2)求证:PD=QD.

【答案】(1)58°;(2)证明见解析.
【解析】试题分析:作PF∥BC交AC于F,先证明△APF是等边三角形,得出AP=AF=PF.证出PF=CQ,由ASA证明△PFD≌△QCD,得出对应边相等即可.
试题解析:(1)解:∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,
∵∠Q=28°,
∴∠EDP=∠CDQ=∠ACB﹣∠Q=32°,
∵PE⊥AC,
∴∠PED=90°,
∴∠EPD=90°﹣∠EDP=58°;
(2)证明:作PF∥BC交AC于F,如图所示:
∴∠APF=∠B=60°,∠AFP=∠ACB=60°,
∠FPD=∠CQD,∠PFD=∠QCD,
∴∠APF=∠AFP=∠A=60°,
∴△APF是等边三角形,
∴AP=AF=PF.
∵CQ=AP,
∴PF=CQ,
在△PFD和△QCD中,
∠FPD=∠CQD,PF=CQ,∠PFD=∠QCD
∴△PFD≌△QCD(ASA),
∴PD=QD.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,正确的是( )
A. 任何有理数的偶数次方都是正数
B. 任何一个整数都有倒数
C. 若b=a,则|b|=|a|
D. 一个正数与一个负数互为相反数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B的平分线与∠C的外角的平分线交于P点,PD⊥AC于D,PH⊥BA于H,(1)若点P到直线BA的距离是5cm,求点P到直线BC的距离;(2)求证:点P在∠HAC的平分线上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=A1B,A1C=A1A2,A2D=A2A3,A3E=A3A4,∠B=20°,则∠A4=( )

A. 10° B. 15° C. 30° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列算式:(1)3a+2b=5ab;(2)5y2﹣2y2=3;(3)7a+a=7a2;(4)4x2y﹣2xy2=2xy中正确的有( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com