
【题目】已知四边形ABCD是正方形,△DEF是等腰直角三角形,DE=DF,M是EF的中点.

(1)如图1,当点E在AB上时,求证:点F在直线BC上.
(2)如图2,在(1)的条件下,当CM=CF时,求证:∠CFM=22.5°
(3)如图3,当点E在BC上时,若CM=2,则BE的长为 (直接写出结果)(注:等腰直角三角形三边之比为1:1:![]() )
)
【答案】(1)详见解析;(2)详见解析;(3)2![]()
【解析】
(1)根据四边形ABCD是正方形,△DEF是等腰直角三角形,利用SAS证明△ADE≌△CDF即可;
(2)作EN∥CM交BC于N,根据M是EF的中点得CM是△EFN的中位线,可证得△BEN是等腰直角三角形,利用外角的性质即可求证;
(3)过点F作FG⊥BC于G,FQ⊥AD于Q,过点E作EH⊥AD于H,则四边形CGQD为矩形,EH=AB=CD,作FN∥CM交CG于N,可根据AAS证明△QDF≌△HED,可得矩形CGQD是正方形,连接DM、GM,则DM是Rt△EDF的中线、GM是Rt△EGF的中线,可根据SSS证明△CMD≌△CMG,得到△NGF是等腰直角三角形,即可求出结果.
(1)证明:∵四边形ABCD是正方形,
∴AD=CD=AB=BC,∠A=∠BCD=∠ADC=90°,
∵△DEF是等腰直角三角形,
∴∠EDF=90°,
∴∠ADC=∠EDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中, ,
,
∴△ADE≌△CDF(SAS),
∴∠A=∠DCF=90°,
∴点F在直线BC上;
(2)证明:作EN∥CM交BC于N,如图2所示:
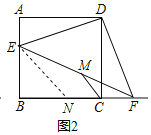
∵M是EF的中点,EN∥CM,
∴CM是△EFN的中位线,∠BCM=∠BNE,
∴CN=CF,由(1)得:△ADE≌△CDF,
∴AE=CF,
∴AE=CN,
∴BE=BN,
∴△BEN是等腰直角三角形,
∴∠BNE=45°,
∴∠BCM=45°,
∵CM=CF,
∴∠CMF=∠CFM=![]() ∠BCM=22.5°;
∠BCM=22.5°;
(3)解:过点F作FG⊥BC于G,FQ⊥AD于Q,则四边形CGQD为矩形,
过点E作EH⊥AD于H,则EH=AB=CD,
作FN∥CM交CG于N,如图3所示:
∵∠EDF=90°,
∴∠HDE+∠QDF=90°,
∵∠HDE+∠HED=90°,
∴∠QDF=∠HED,
在△QDF和△HED中,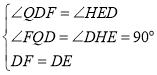 ,
,
∴△QDF≌△HED(AAS),
∴EH=DQ,
∴DQ=CD,
∴矩形CGQD是正方形,
∴CG=BC,
∵M是EF的中点,FN∥CM,
∴CM是△ENF的中位线,
∴∠GCM=∠GNF,NF=2CM=4,CE=CN,
∴BE=NG,
连接DM、GM,则DM是Rt△EDF的中线、GM是Rt△EGF的中线,
∴DM=![]() EF,GM=
EF,GM=![]() EF,
EF,
∴DM=GM,
在△CMD和△CMG中,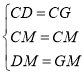 ,
,
∴△CMD≌△CMG(SSS),
∴∠DCM=∠GCM=![]() ∠DCG=45°,
∠DCG=45°,
∴∠GNF=45°,
∴△NGF是等腰直角三角形,
∴NG=![]() NF=
NF=![]() ,
,
故答案为:![]() .
.



科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
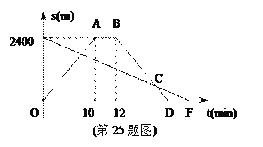
【题目】小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象。
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是抛物线![]() 图象的一部分,已知抛物线的对称轴是
图象的一部分,已知抛物线的对称轴是![]() ,与
,与![]() 轴的一个交点是
轴的一个交点是![]() ,有下列结论:
,有下列结论:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④抛物线与![]() 轴的另一个交点是
轴的另一个交点是![]() ;
;
⑤点![]() ,
,![]() 都在抛物线上,则有
都在抛物线上,则有![]() .
.
其中正确的是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、图②均是5×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、E、F均在格点上.在图①、图②中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
(1)在图①中画一个正方形ABCD,使其面积为5.
(2)在图②中画一个等腰△EFG,使EF为其底边.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com