
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是( )

A. ②③ B. ②④ C. ②③④ D. ①③④
【答案】C
【解析】
OA不一定等于OD;由AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,根据角平分线的性质,可得DE=DF,继而证得AE=AF,则可得AD是EF的垂直平分线;判定AD⊥EF;又由当∠BAC=90°时,可得四边形AEDF矩形,继而证得四边形AEDF是正方形;由AE=AF,DE=DF,即可判定AE2+DF2=AF2+DE2.
∵AD是EF的垂直平分线,
∴OE=OF,OA不一定等于OD,故①错误;
∵AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,
∴DE=DF,
∵∠ADE=90°-∠DAE,∠ADF=90°-∠DAF,
∴∠ADE=∠ADF,
∴AE=AF,
∴点A在EF的垂直平分线上,点D在EF的垂直平分线上,
∴AD是EF的垂直平分线,
即AD⊥EF,故②正确;
∵∠AED=∠EFD=90°,
∴当∠A=90°时,四边形AEDF是矩形,
∵DE=DF,
∴四边形AEDF是正方形,故③正确;
∵AE=AF,DE=DF,
∴AE2+DF2=AF2+DE2,∴④正确,
所以正确的是:②③④,
故选C.


科目:初中数学 来源: 题型:
【题目】在直角三角形中,两直角边的平方和等于斜边的平方.如图1,若在△ABC中,∠C=90°,则AC2+BC2=AB2.我们定义为“商高定理”.
(1)如图1,在△ABC中,∠C=90°中,BC=4,AB=5,试求AC=__________;
(2)如图2,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.试证明:AB2+CD2=AD2+BC2;
(3)如图3,分别以Rt△ACB的直角边BC和斜边AB为边向外作正方形BCFG和正方形ABED,连结CE、AG、GE.已知BC=4,AB=5,求GE2的值.
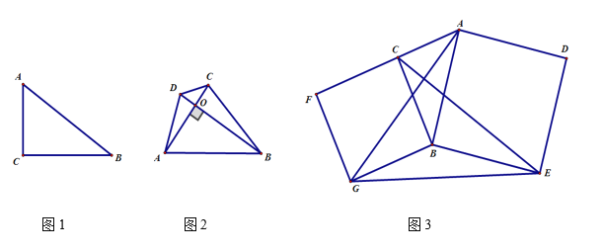
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AB=AC,D是BC上一点,点E、F分别在AB、AC上,BD=CF,CD=BE,G为EF的中点.

求证:(1)△BDE≌△CFD(2)DG⊥EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王师傅非常喜欢自驾游,为了解他新买的轿车的耗油情况,将油箱加满后进行了耗油实验,得到下表中的数据:
轿车行驶的路程 |
|
|
|
|
| ······ |
油箱中的剩余油量 |
|
|
|
|
| ····· |
(1)在这个问题中,自变量是_ 因变量是_ ;
(2)该轿车油箱的容量为__ L,行驶![]() 时,估计油箱中的剩余油量为____
时,估计油箱中的剩余油量为____![]() ;
;
(3)王师傅将油箱加满后,驾驶该轿车从![]() 地前往
地前往![]() 地,到达
地,到达![]() 地时油箱中的剩余油量为
地时油箱中的剩余油量为![]() ,请估计
,请估计![]() 两地之间的距离.
两地之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=![]() ,求CG的长度;
,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(1)如图1,当∠ACD=45°时,求证:DE是⊙O的切线;
(2)如图2,当点F是CD的中点时,求△CDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各顶点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出A′、B′、C′的坐标,并在图中画出平移后图形;
(3)求出△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com