
例题:若 ,求
,求
解:因为
所以
所以
所以
所以
问题(1)若 ;
;
问题(2)已知 是△ABC的三边长,满足
是△ABC的三边长,满足 ,
, 是△ABC中最长边的边长,且
是△ABC中最长边的边长,且 为整数,那么
为整数,那么 可能是哪几个数?
可能是哪几个数?
(1)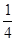 ;
;
【解析】
试题分析:(1)先根据完全平方公式配方得(x-y)2+(y+2)2=0,再根据非负数的性质求得x、y的值,最后根据有理数的乘方法则计算即可;
(2)先移项,再根据完全平方公式配方得(a-5)2+(b-4)2=0,然后根据非负数的性质求得a、b的值,最后根据三角形的三边关系求解即可.
(1)x2-2xy+2y2+4y+4=x2-2xy+y2+y2+4y+4=(x-y)2+(y+2)2=0,
∴x-y=0,y+2=0,解得x=-2,y=-2,
∴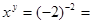
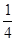 ;
;
(2)∵a2+b2=10a+8b-41,
∴a2-10a+25+b2-8b+16=0,即(a-5)2+(b-4)2=0,
∴a-5=0,b-4=0,解得a=5,b=4,
∵c是△ABC中最长的边,
∴5≤c<9
∴c的取值可以是:5、6、7、8.
考点:完全平方公式,非负数的性质,三角形的三边关系
点评:解题的关键是熟练掌握非负数的性质:若两个非负数的和为0,这两个数均为0;三角形的三边关系:任两边之和大于第三边,任两边之差小于第三边.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:阅读理解
|
|
|
|
| ||
|
| ||
|
| α+β | ||
|
| -3 |
| 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 16(2m+n) |
| m-n-1 | m+7 |
| 16(2m+n) |
| m-n-1 | m+7 |
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 说理填空:如图,点E是DC的中点,EC=EB,∠CDA=120°,DF∥BE,且DF平分∠CDA,若△BCE的周长为18cm,求DC的长.
说理填空:如图,点E是DC的中点,EC=EB,∠CDA=120°,DF∥BE,且DF平分∠CDA,若△BCE的周长为18cm,求DC的长.| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com