
【题目】某家电商场计划用9万元从生产厂家购进50台电视机,已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.
(1)若家电商场同时购进两种不同型号的电视机共50台,用去9万元,请你计算一下商场有哪几种进货方案?
(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,应选择哪种方案?
【答案】(1)有两种进货方案:购进A种25台,B种25台或购进A种35台,C种15台;(2)选择购A、C两种型号的电视机,理由见解析.
【解析】
(1)分三种情况讨论:①只购进A、B两种型号,②只购进B、C两种型号,③只购进A、C两种型号,分别列出方程求解;
(2)分别计算(1)中进货方案获得的利润,选择利润最多的方案即可.
解:(1)只购进A、B两种型号时,设购进A型![]() 台,则B型(50-
台,则B型(50-![]() )台,
)台,
1500![]() +2100(50-
+2100(50-![]() )=90000,
)=90000,
解得![]() =25,50-
=25,50-![]() =25台.
=25台.
只购进B、C两种型号时,设购进B型![]() 台,则C型(50-
台,则C型(50-![]() )台,
)台,
2100![]() +2500(50-
+2500(50-![]() )=90000,
)=90000,
解得![]() =87.5(舍去)
=87.5(舍去)
只购进A、C两种型号时,设购进A型z台,则C型(50-z)台,
1500![]() +2500(50-
+2500(50-![]() )=90000,
)=90000,
解得![]() =35,50-
=35,50-![]() =15台
=15台
所以有两种进货方案:购进A种25台,B种25台或购进A种35台,C种15台.
(2)当只购A、B两种型号时,利润:25×150+25×200=8750元
当只购A、C两种型号时,利润:35×150+15×250=9000元
所以选择购A、C两种型号的电视机.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中,且A![]() 、B
、B![]() 、C
、C![]() .将其平移后得到
.将其平移后得到![]() ,若A,B的对应点是
,若A,B的对应点是![]() ,
,![]() ,C的对应点
,C的对应点![]() 的坐标是
的坐标是![]() .
.
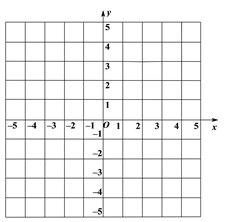
(1)在平面直角坐标系中画出△ABC;
(2)写出点![]() 的坐标是_____________,
的坐标是_____________,![]() 坐标是___________;
坐标是___________;
(3)此次平移也可看作![]() 向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将![]() 化为分数形式,
化为分数形式,
由于![]() ,设
,设![]() ,①
,①
得![]() ,②
,②
②①得![]() ,解得
,解得![]() ,于是得
,于是得![]() .
.
同理可得![]() ,
,![]() .
.
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(类比应用)
(1)![]() ;
;
(2)将![]() 化为分数形式,写出推导过程;
化为分数形式,写出推导过程;
(迁移提升)
(3)![]() ,
,![]() ;(注
;(注![]() ,
,![]() )
)
(拓展发现)
(4)若已知![]() ,则
,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.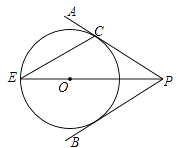
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;② ![]() ;③ac-b+1=0;④OA·OB=
;③ac-b+1=0;④OA·OB= ![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )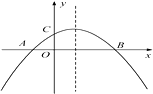
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC与点E,将△BCE绕点C顺时针旋转90°得到△DCF,若CE=1 cm,则BF=cm.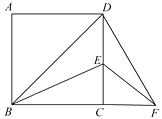
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一批共享单车需要维修,维修后继续投放骑用,现有甲、乙两人做维修,甲每天维修16辆,乙每天维修的车辆比甲多8辆,甲单独维修完成这批共享单车比乙单独维修完多用20天,公司每天付甲80元维修费,付乙120元维修费.
(1)问需要维修的这批共享单车共有多少辆?
(2)在维修过程中,公司要派一名人员进行质量监督,公司负担他每天10元补助费,现有三种维修方案:①由甲单独维修;
②由乙单独维修;
③甲、乙合作同时维修,你认为哪种方案最省钱,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com